Safe Reinforcement Learning for Robotics: From Exploration to Policy Learning
Puze Liu
German Research Center for AI - DFKI
System AI for Robot Learning - SAIROL

Advances in Robot Learning
Robot Soccer (2023), Deepmind
Humanoid Backflip (2024), Unitree
Robot Soccer (2023), Deepmind
Humanoid Backflip (2024), Unitree
Robot Air Hockey (2023), PUT & TU Darmstadt
Failures
Training pipeline
- Policy trained in simulation or using pre-collected dataset
- Domain randomization or data augmentation to increase the robustness
- Zero shot transfer without real-world fine tuning
- Simulator that captures environment variations
- Failure in unforeseen scenarios
- Robot lacks of performance improving capability
Problems
Keep robots learning while interacting with the real world!
REINFORCEMENT LEARNING
Sample Efficiency Exploration SAFETY
Safe Reinforcement Learning
$$ \begin{aligned} \max_{\pi} \quad \mathbb{E}_{\tau \sim \pi} \left[\sum_{t=0} \gamma^t r(s_t, a_t) \right] \quad \quad \text{s.t.} \quad \mathcal{K}(\pi) \leq \eta \end{aligned} $$
Safe Exploration
- Safely learning a policy throughout training process
- Enables training on the real robot
- Require extensive domain knowledge (constraints, dynamics, or backup policy)
- Not scalable to complex systems
$ \mathcal{K}(\pi) \mathrel{:=} k(s_t, \pi(s_t)) \leq 0, \quad \forall t$
Safe Policy Learning
- Learn a safe policy by the end of the training
- Lower requirements for domain knowledge
- Generalizable across various tasks
- Sensitive to the mismatch of state-action distribution
$\mathcal{K}(\pi) \mathrel{:=} \mathbb{E}_{\tau \sim \pi} \left[\sum_{t=0} \gamma^t k(s_t, a_t) \right] \leq \eta$
Core Question
What is the relationship between amount of domain knowledge
required
and the level of safety it
provides in the context of SafeRL for robotics
Safe Exploration
- Safely learning a policy throughout training process
- Enables training on the real robot
- Require extensive domain knowledge (constraints, dynamics, or backup policy)
- Not scalable to complex systems
$ \mathcal{K}(\pi) \mathrel{:=} k(s_t, \pi(s_t)) \leq 0, \quad \forall t$
Safe Policy Learning
- Learn a safe policy by the end of the training
- Lower requirements for domain knowledge
- Generalizable across various tasks
- Sensitive to the mismatch of state-action distribution
$\mathcal{K}(\pi) \mathrel{:=} \mathbb{E}_{\tau \sim \pi} \left[\sum_{t=0} \gamma^t k(s_t, a_t) \right] \leq \eta$
Key Components
Constraints
Dynamics
Constraints
Dynamics
Known
Known
Safe Exploration
Constraints
Dynamics
Known
Known
Safe Exploration
Learned / Learnable
Known
Safe Exploration /
Policy Learning
Constraints
Dynamics
Known
Known
Safe Exploration
Learned / Learnable
Known
Safe Exploration /
Policy Learning
Safety Critic
Unknown
Safe Policy Learning
Safe Exploration
Problem Formulation
$$ \max_{\pi} \quad \underset{\tau \sim \pi}{\mathbb{E}} \left[\sum_{t=0} \gamma^t r(s_t, a_t) \right] \quad \quad \text{s.t.} \quad k(s_t) < 0, \quad \forall t $$
Control Affine Dynamics $ \quad \quad \quad \dot{\vs} = f(\vs) + G(\vs) \vu $
Safe Set $ \mathcal{S}_{\text{S}} = \{ \vs \in \mathcal{S} : k(\vs) < 0 \} $
Constraint Manifold in Augmented State Space $$ \MM = \left\{(\vs, \vmu) \;|\; k(\vs) + \vmu = 0 \right\} $$
with $\vmu > 0$
Safe Set $$ \mathcal{S}_{\text{S}} = \{ \vs \in \mathcal{S} : k(\vs) < 0 \} $$
Constraint Manifold in Augmented State Space $$ \MM = \left\{(\vs, \vmu) \;|\; k(\vs) + \vmu = 0 \right\} $$
with $\vmu > 0$
Dynamics for Slack Variable $$\dot{\vmu} = A(\vmu) \vu_{\mu}$$ $A$ is continuous, strictly increasing and $A(\vzero) = \vzero$
Dynamics of the Augmented System $$\begin{bmatrix}\dot{\vs} \\ \dot{\vmu} \end{bmatrix} = \begin{bmatrix} f(\vs) \\ \vzero \end{bmatrix} + \begin{bmatrix} G(\vs) & \vzero \\ \vzero & A(\vmu) \end{bmatrix} \begin{bmatrix} \vu_s \\ \vu_{\mu} \end{bmatrix}$$
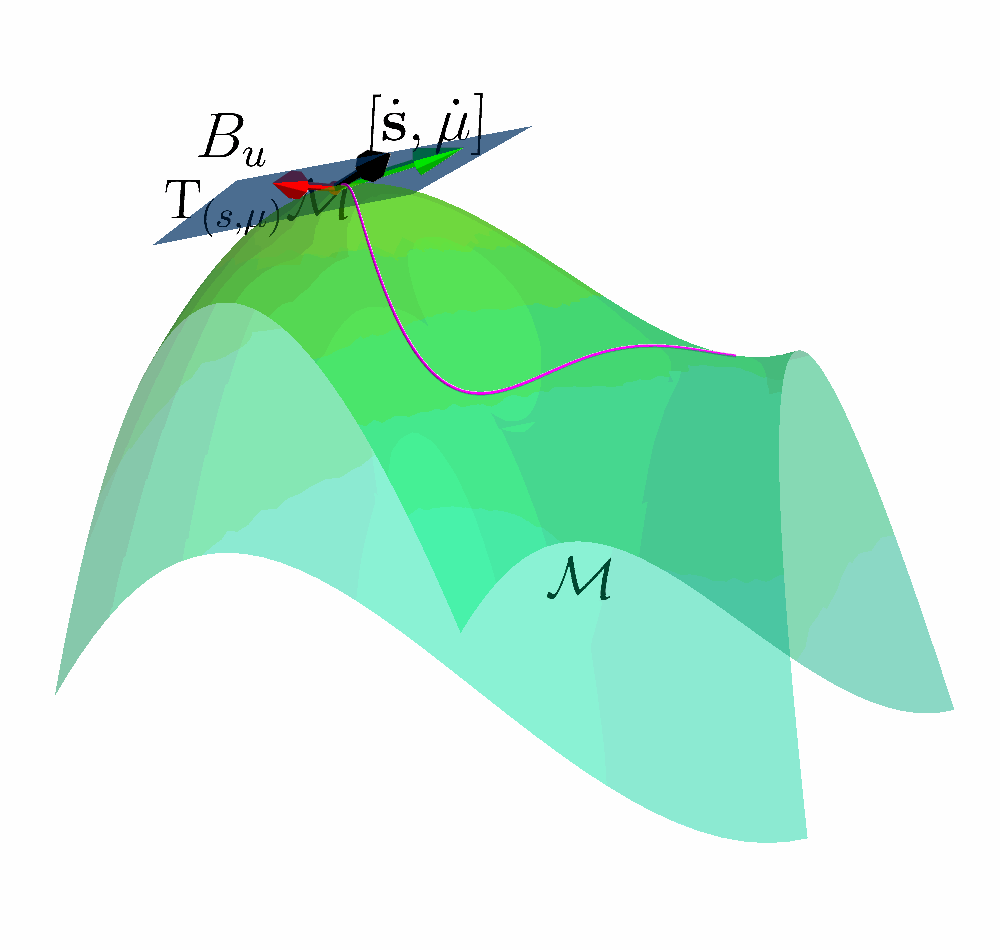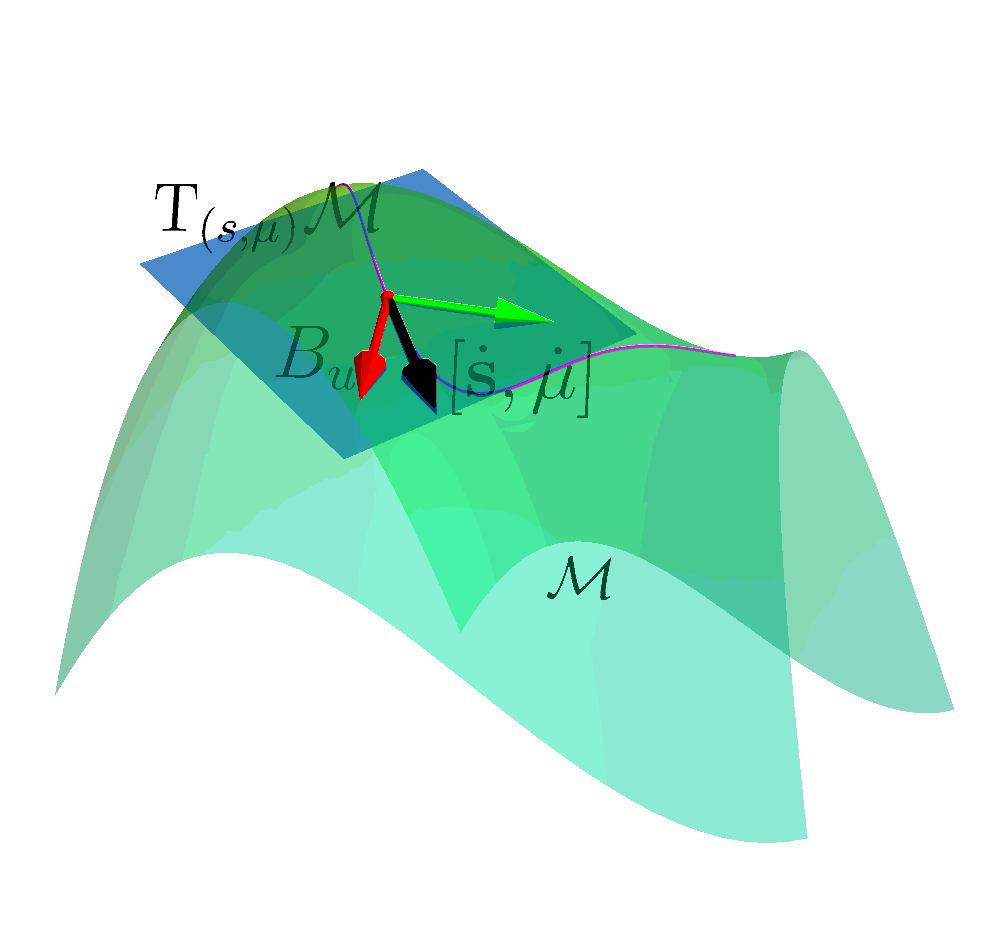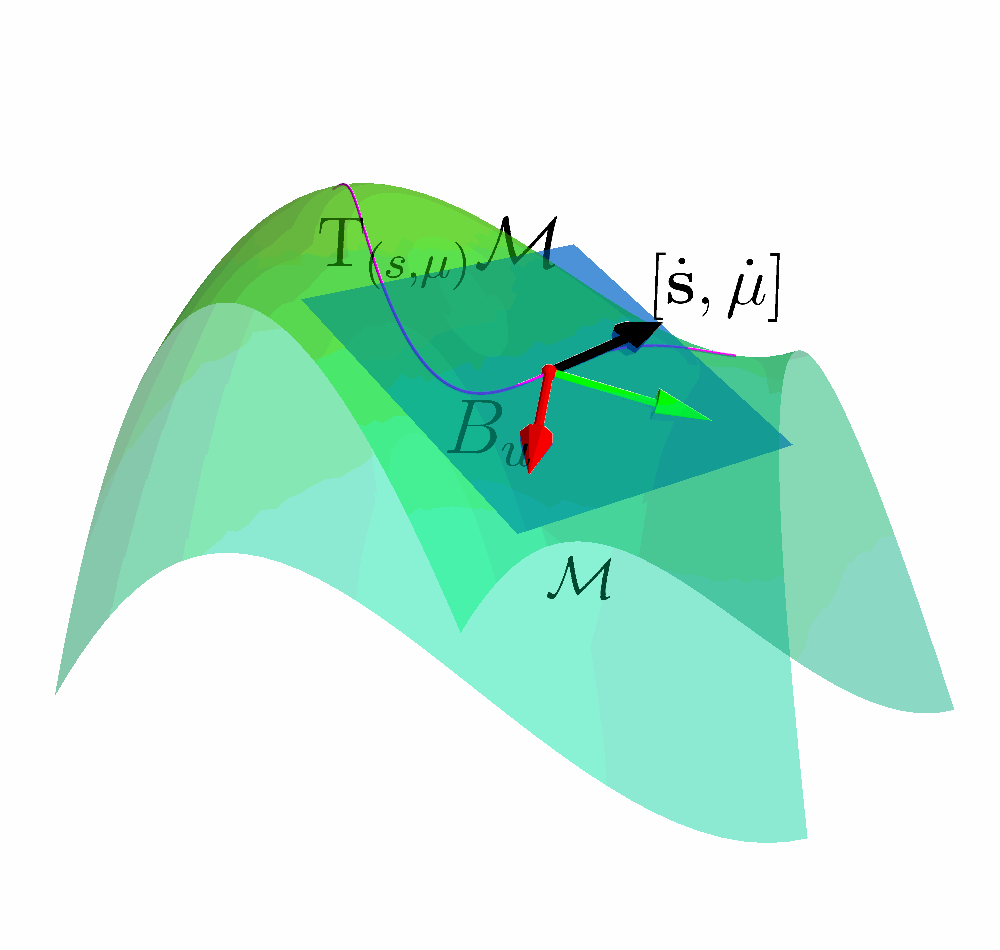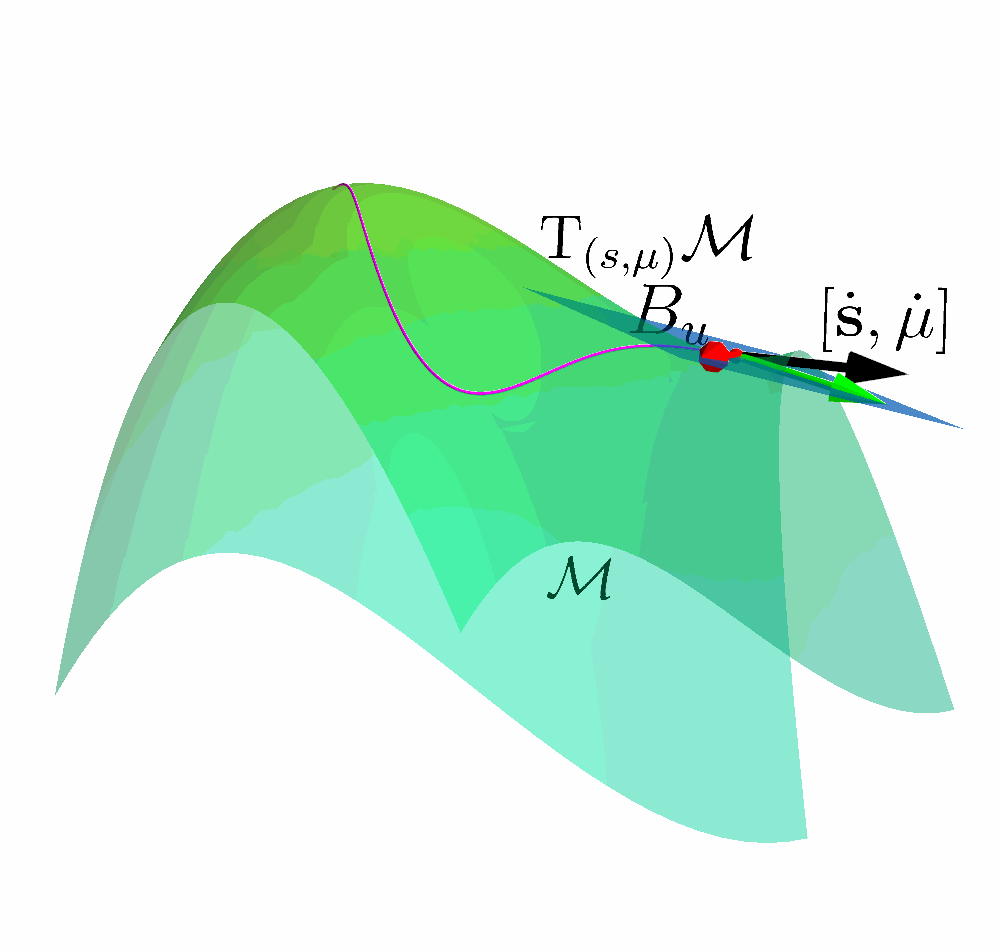
Tangent Space of the Constraint Manifold
Constraint Manifold in Augmented State Space $$ \MM = \left\{(\vs, \vmu) \;|\; k(\vs) + \vmu = 0 \right\} $$
Tangent Space $$\mathrm{T}_{(s, \mu)}\MM = \left\{ \vv \;|\; \begin{bmatrix} \mJ_k & \mathbb{I} \end{bmatrix} \vv = \vzero \right \} $$
Let $ \begin{bmatrix} \dot{\vs} & \dot{\vmu} \end{bmatrix}^{\intercal} \in \mathrm{T}_{(s, \mu)}\MM$ and combine with the Augmented Dynamics
$$ \underbrace{\mJ_k\vf}_{\vpsi} + \underbrace{\begin{bmatrix} \mJ_k \mG & \mA \end{bmatrix}}_{\mJ_u} \begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix}= \vzero $$
$$ \underbrace{\mJ_k\vf}_{\vpsi} + \underbrace{\begin{bmatrix} \mJ_k \mG & \mA \end{bmatrix}}_{\mJ_u} \begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix}= \vzero $$
Acting on the TAngent space of the COnstraint Manifold (ATACOM)
$\begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix} = \textcolor{b2e061}{\underbrace{-\mJ_u^{\dagger} \vpsi}_{\text{Drift Comp.}}}$ $\textcolor{#fd7f6f}{\underbrace{- \lambda \mJ_u^{\dagger} \vc}_{\text{ Contraction }}}$ $\textcolor{7eb0d5}{\underbrace{+ \mB_u \va }_{\text{ Tangential }}} $
ATACOM-Controller
Acting on the TAngent space of the COnstraint Manifold (ATACOM)
$\begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix} = \textcolor{b2e061}{\underbrace{-\mJ_u^{\dagger} \vpsi}_{\text{Drift Comp.}}}$ $\textcolor{#fd7f6f}{\underbrace{- \lambda \mJ_u^{\dagger} \vc}_{\text{ Contraction }}}$ $\textcolor{7eb0d5}{\underbrace{+ \mB_u \va }_{\text{ Tangential }}} $
- $ \mB_u = \begin{bmatrix} \vb_1 \; \cdots \; \vb_2 \end{bmatrix} $ span the nullspace of $\mJ_u$ and determines the tangent space basis, such that $\mJ_u \mB_u = \vzero$.
- ATACOM constructs a safe action space $\va \in \mathcal{A}$ and a mapping $W(\va): \mathcal{A} \rightarrow \mathcal{U}$.
- Can be used in various RL methods as all actions are sampled in the safe action space.
Acting on the TAngent space of the COnstraint Manifold (ATACOM)
$\begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix} = \textcolor{b2e061}{\underbrace{-\mJ_u^{\dagger} \vpsi}_{\text{Drift Comp.}}}$ $\textcolor{#fd7f6f}{\underbrace{- \lambda \mJ_u^{\dagger} \vc}_{\text{ Contraction }}}$ $\textcolor{7eb0d5}{\underbrace{+ \mB_u \va }_{\text{ Tangential }}} $
Dynamics: $ \;\quad \dot{s} = -1 + u_s $
Constraint: $ \quad s^2 < 1 $
$ \begin{aligned} \MM &= \{(s, \mu) | s^2 + \mu -1 = 0 \} \\ \psi &= 0, \quad a=1, \quad \dot{\mu} = \mu u_{\mu} \\ J_u & = \begin{bmatrix} 2s & \mu \end{bmatrix}, \quad B_u=\begin{bmatrix} -\mu \\ 2s \end{bmatrix} \end{aligned}$

Air Hockey Experiment
- Task: Hit the randomly initialized puck to the goal
- Control: Robot's joint velocity
- Constraints:
- Mallet stays on the table surface and within the boundary (5 Dim)
- Robot's elbow and wrist do not collide with the table (2 Dim)
- Joint position limits (14 Dim)
Trained policy in simulation
Training directly in the real world
- Total training: 3000 episodes (~24h)
- Resetting System: Mitsubishi PA10 with a vacuum gripper
- Time Efficiency: Collect 100 episodes real-world data using the policy learned in simulation
Resetting system
Success rate
| Simulation | 86% |
| Zero-shot transfer | 12% |
| After training | 71% |
Hitting Velocity
| Simulation | 0.92m/s |
| Zero-shot transfer | 0.97m/s |
| After training | 0.97m/s |
ATACOM - Extensions
Mobile Robot with Differential Drive
Mobile Robot with Differential Drive
Cluttered Environment
Mobile Robot with Differential Drive
Cluttered Environment
Second-Order Dynamics
ATACOM the knowledge of constraints and dynamics to enable robots to explore safely in the real world
Limitations
- Constraints are pre-determined and need to be carefully verified for each task
- Require the full knowledge of the dynamic systems
Constraints
Dynamics
ATACOM
Known
Known
Safe Exploration
Learned / Learnable
Known
Safe Exploration /
Policy Learning
Safety Critic
Unknown
Safe Policy Learning
Safe Human Robot Interaction
Collision Avoidance Problem
Distance-based constraint
$$d(p_{\text{r}}, p_{\text{o}}) > \eta $$
- Complex geometries
- Dynamic human motion
- Accurate in the proximity of the human
- Smooth / differentiable distance function
- Fast computation
Distance-Based Constraint
$$d(p_{\text{r}}, p_{\text{o}}) > \eta $$
Primitives (Spheres, Cylinders)
- Simple Computation
- Globally Well-Defined
- Poor Scalibility for Complex Geometries
- Non-Smooth Distance Function
Function Approximator (NN)
- Powerful Local Representation
- Handle Complex Shapes
- Poor Extrapolating Ability



(Chabra et al., 2020)
ReDSDF - Regularized Deep Signed Distance Field
- Simple Computation
- Globally Well-Defined
- Powerful Local Representation
- Handle Complex Shapes
Poor Extrapolating AbilityPoor Scalibility for Complex GeometriesNon-Smooth Distance Function- Articulated Objects
$$ d_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq}) = \left[1-\sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\right]\textcolor{LightGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\textcolor{skyblue}{\underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
$ \sigma_{\vtheta}(\vx, \vq) = \sigmoid\left(\textcolor{OrangeRed}{\alpha_{\vtheta}}\left( \lVert\vx - \vx_c\rVert_2 - \textcolor{OrangeRed}{\rho_{\vtheta}} \right)\right) $
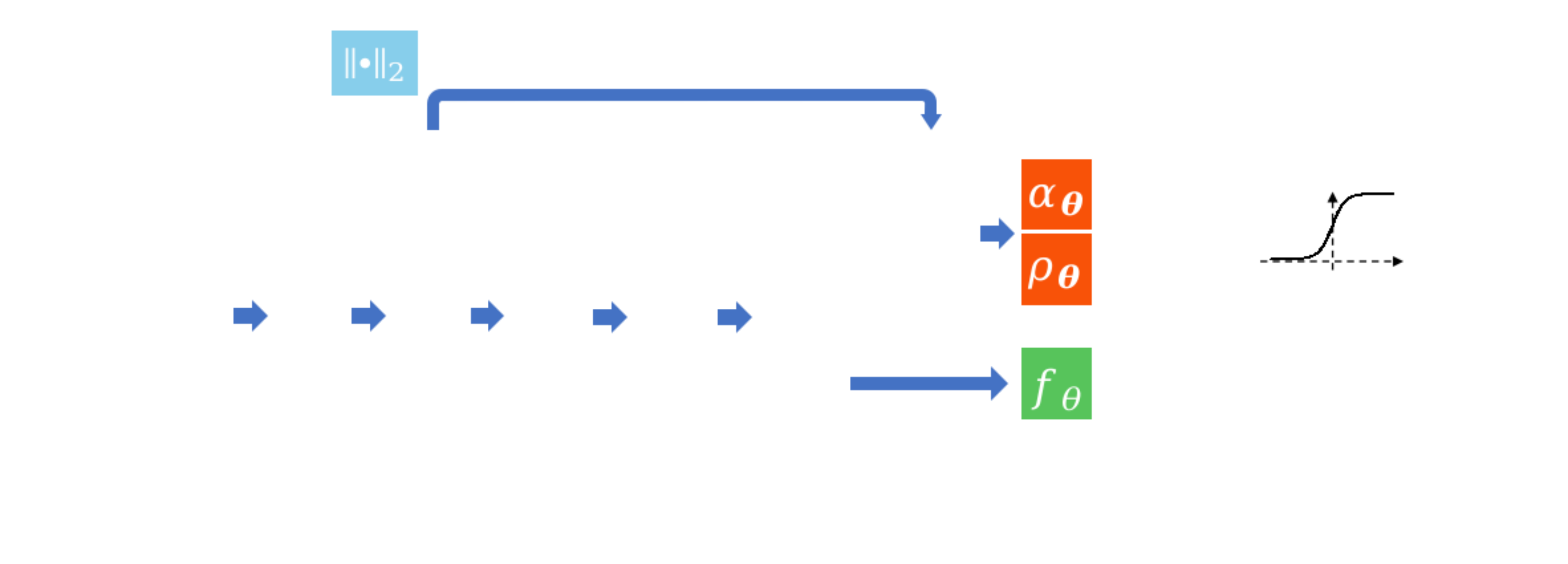
ReDSDF Reconstruction


Table
Shelf




Table
Shelf
Tiago
Human
ReDSDF Extrapolation

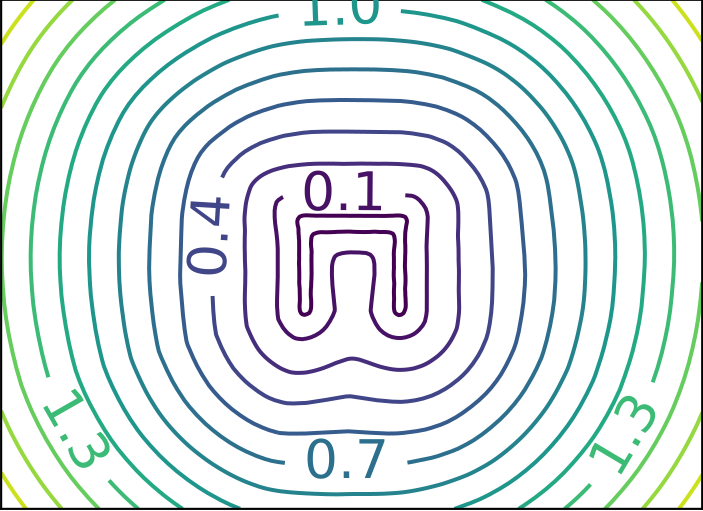
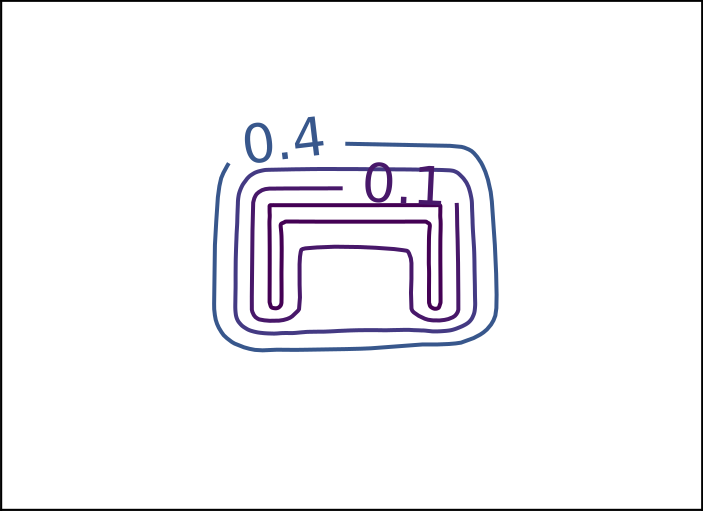
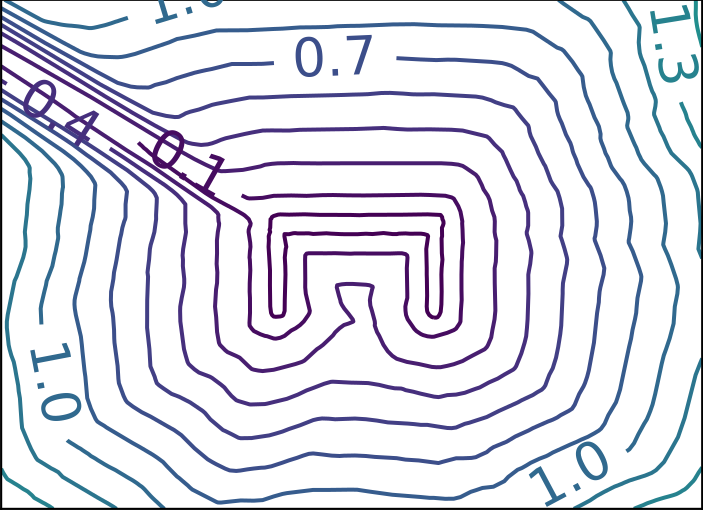

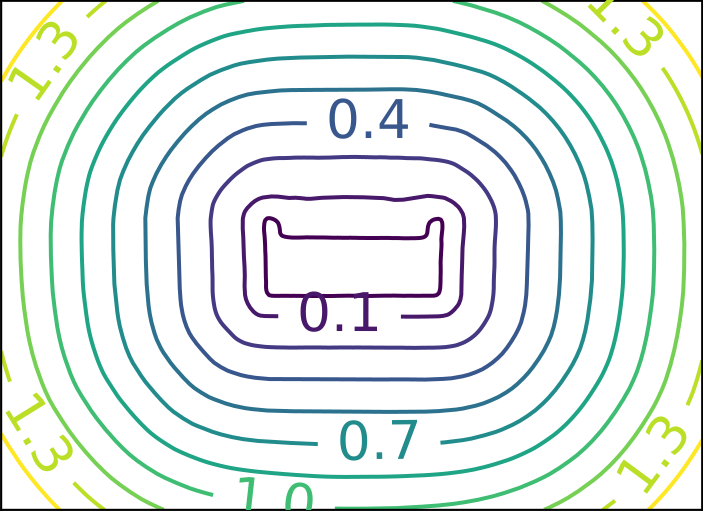
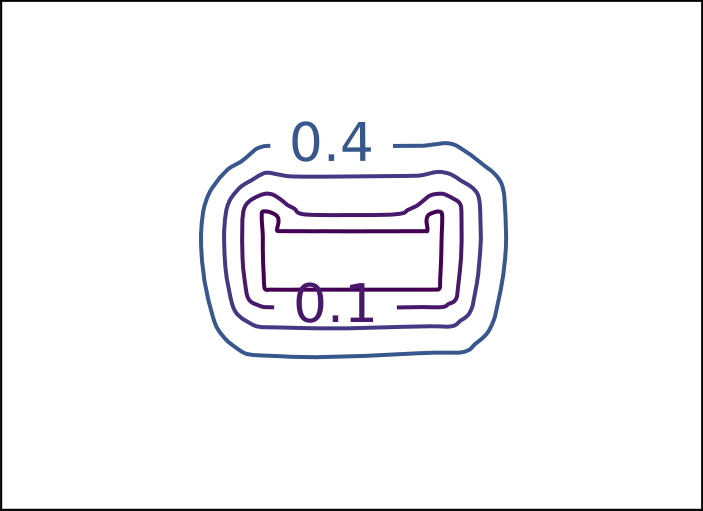
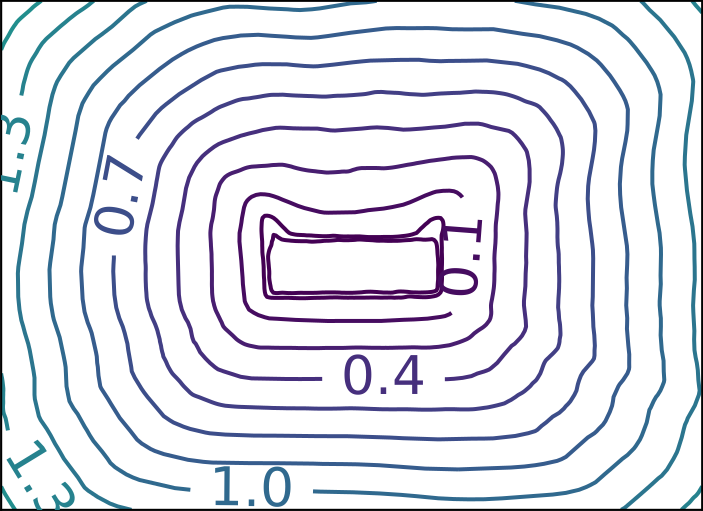


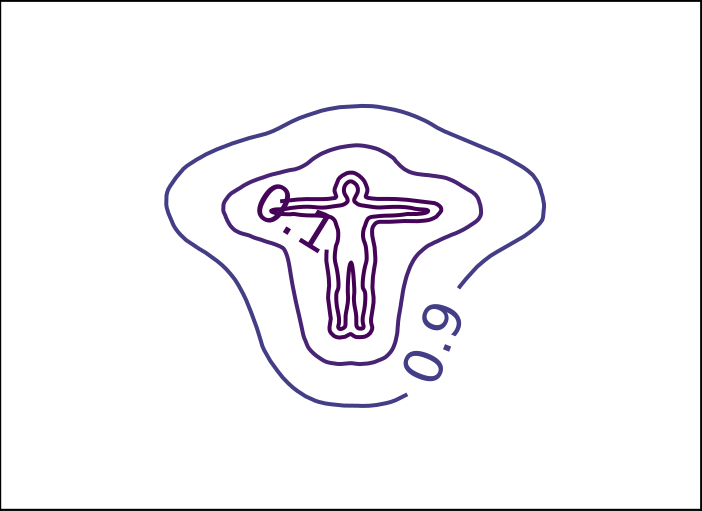
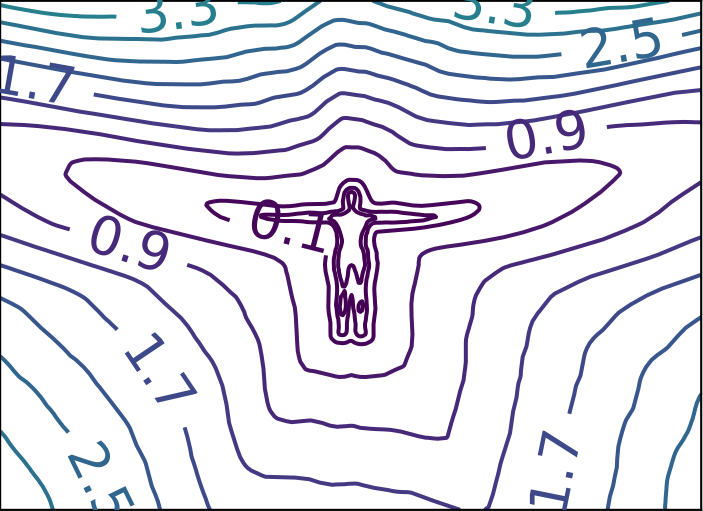
Ground Truth
ReDSDF
DeepSDF
ECoMaNN
ReDSDF + ATACOM for HRI
ReDSDF + ATACOM for HRI
3x speed
Long-Term Safety and Uncertainty
Limitations
- Constraints are pre-trained for specialized task
- Need to generate dataset to cover various human/robot motions
- Do not consider the long-term safety
Limitations
- Constraints are pre-trained for specialized task
- Need to generate dataset to cover various human/robot motions
- Do not consider the long-term safety
- Require full knowledge of environment dynamics
- Uncertainty of the estimation and the environment
Distributional Feasibility Value Function
Construct with a Distributional Safety Value Function that accounts for long-term safety and uncertainty
Construct with a Distributional Safety Value Function that accounts for long-term safety and uncertainty
Feasibility Value Function
$$ V^{\pi}_{F}(s) = \mathbb{E}_{\pi}\left[ \sum_{t=0} \gamma^t \max(k(s_t), 0) | s_0 = s \right] $$
Bellman Equation
$$ V^{\pi}_{F}(s) = \max(k(s), 0) + \gamma \mathbb{E}_{s'}\left[V^{\pi}_{F}(s') \right] $$
Construct with a Distributional Safety Value Function that accounts for long-term safety and uncertainty
Feasibility Value Function
$$ V^{\pi}_{F}(s) = \mathbb{E}_{\pi}\left[ \sum_{t=0} \gamma^t \max(k(s_t), 0) | s_0 = s \right] $$
Bellman Equation
$$ V^{\pi}_{F}(s) = \max(k(s), 0) + \gamma \mathbb{E}_{s'}\left[V^{\pi}_{F}(s') \right] $$
Gaussian Parameterization
$$ V^{\pi}_{F}(s) \sim \mathcal{N}(\mu^{F}(s), \Sigma^{F}(s)) $$
Let $ k'(s) = \max(k(s), 0) $
Distributional Bellman Equation
$$ \begin{split} \mu^{F}(s) &= k'(s) + \gamma \mu^{F}(s') \\ \Sigma^F(s) &= k'(s)^2 + 2 \gamma k'(s) \Sigma^{F}(s') \\ &\;\;\;\; + \gamma^2 \left(\Sigma^{F}(s') + \mu^{F}(s')^2 \right) - \mu^{F}(s)^2 \end{split} $$
Risk-Aware Safety Constraint
(Conditional) Value at Risk of a random variable $Z$
$$ \begin{split} \textcolor{#FF2052}{\text{VaR}}_{\alpha}(Z) &= \inf\{z \in \mathbb{R} | F(z) \geq \alpha \} \\ \textcolor{#03C03C}{\text{CVaR}}_{\alpha}(Z) &= \mathbb{E}[ z \in \mathbb{R} | z \geq \text{VaR}_{\alpha}(Z)]\end{split} $$$F(z)$ is the cumulative distribution function (CDF)
Distributional-ATACOM
$$ \begin{split} \max_{\pi} \quad& \mathbb{E}\left[ \sum_{t}\gamma^t r(s_t, a_t) \right] \\ \text{s.t. } \quad& \text{CVaR}_{\alpha}^{F}(s_t) \leq \eta, \quad \forall t \end{split} $$
Experiments
Planar Air Hockey
Trained Planar Air Hockey
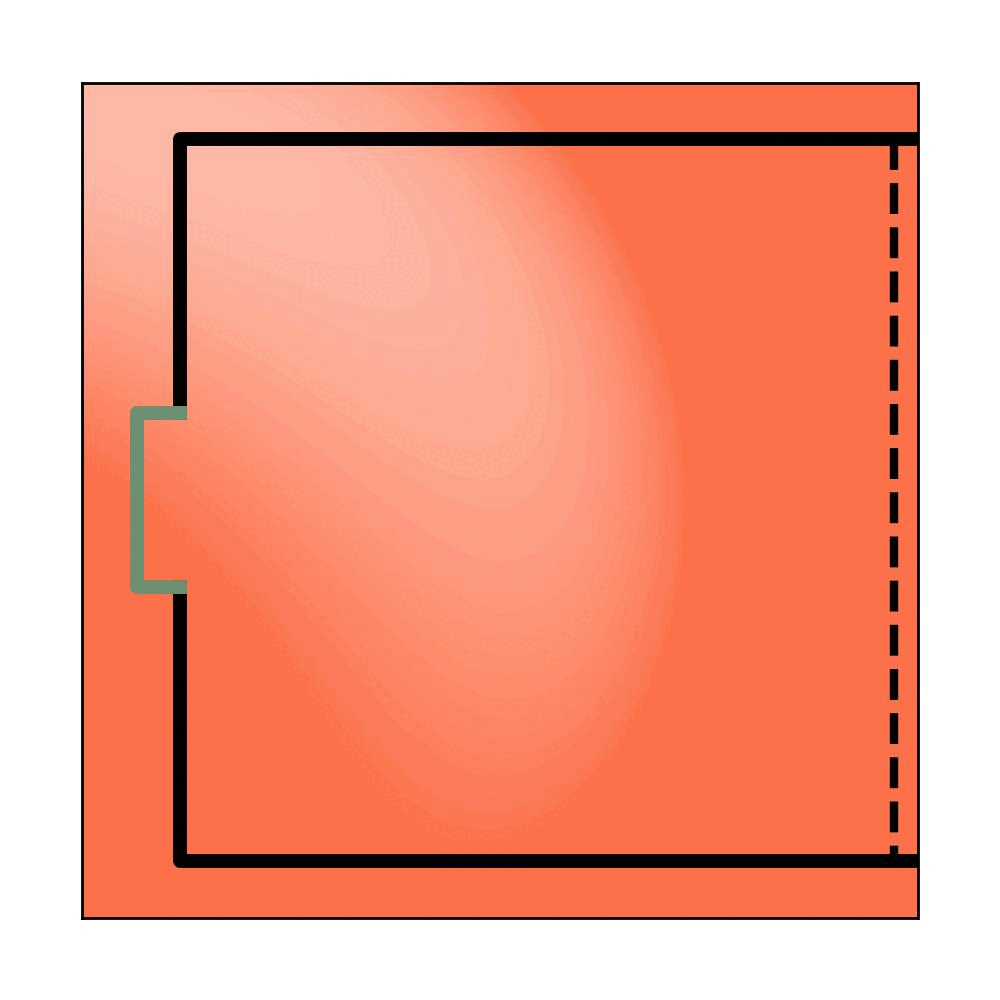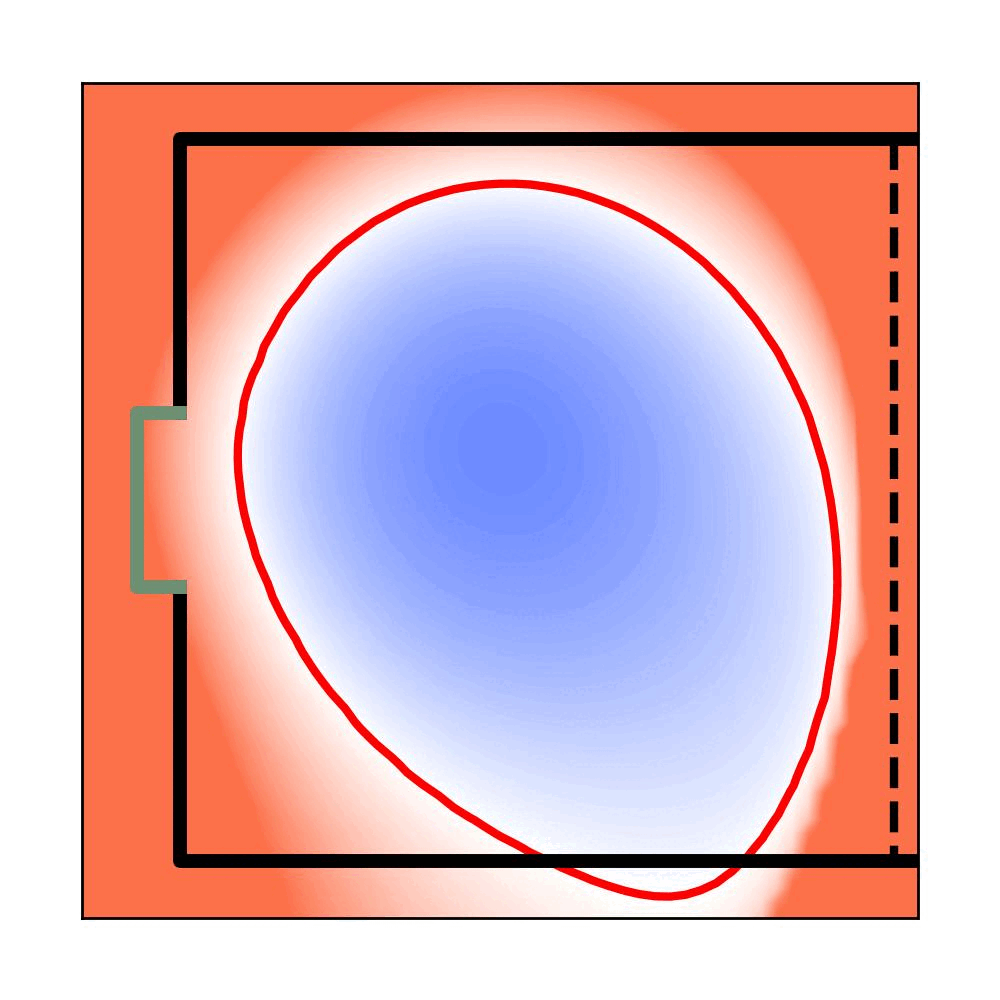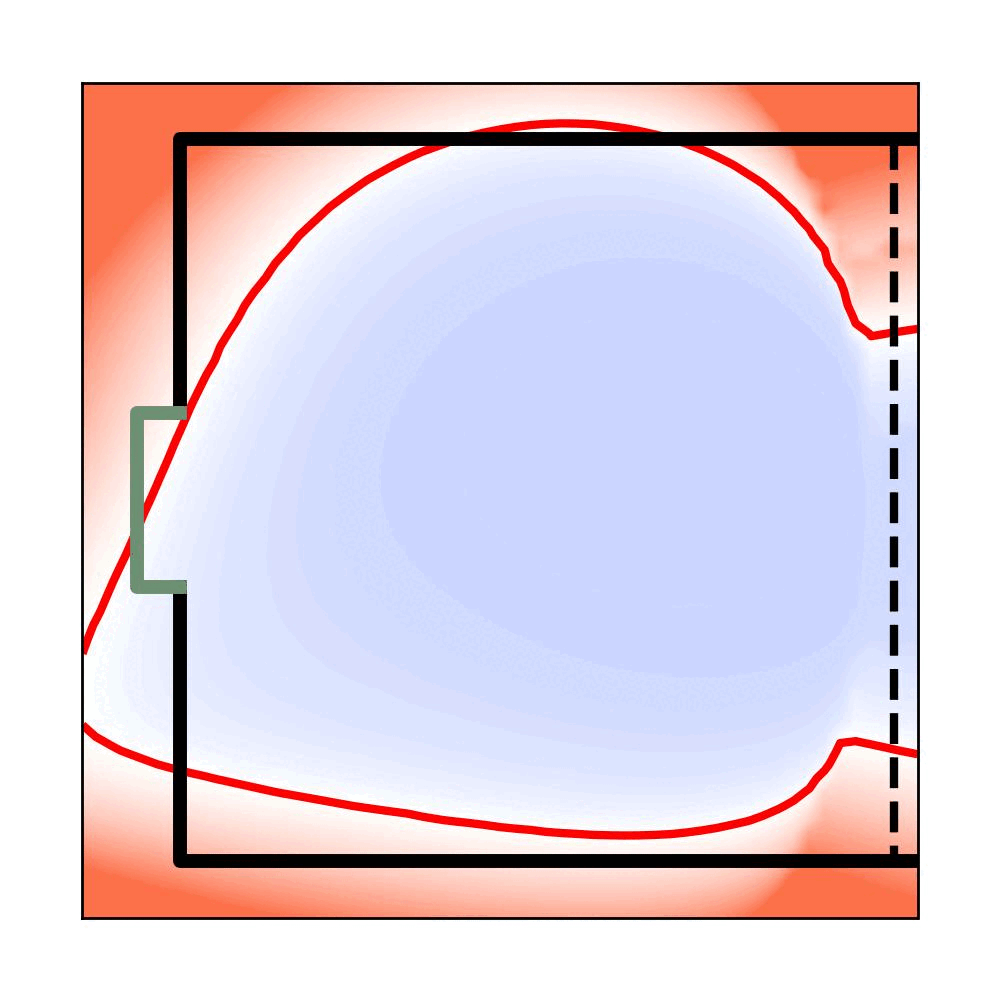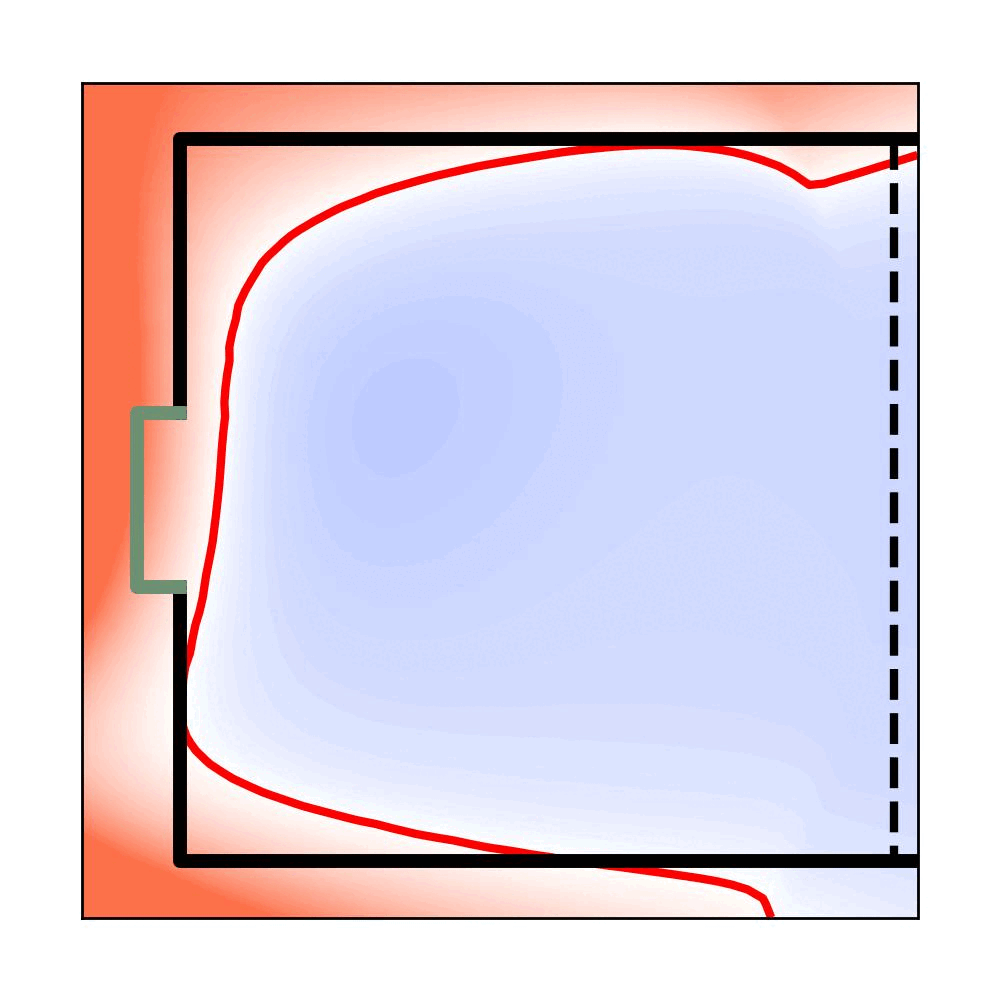
FVF Iteration
Comparison with Baselines
ReDSDF as safety constraint addressing the collision avoidance problem in robotics
Puze Liu,, et al. (2021). Regularized deep signed distance fields for reactive motion generation. IROS
Puze Liu,, et al. (2022). Safe reinforcement learning of dynamic high-dimensional robotic tasks: navigation, manipulation, interaction. ICRA

D-ATACOM builds a learnable safety critic as a constraint on handling long-term safety and uncertainty
Jonas Günster, Puze Liu, et al. (2024). Handling Long-Term Safety and Uncertainty in Safe Reinforcement Learning. CoRL
Constraints
Dynamics
ATACOM
Known
Known
Safe Exploration
ReDSDF /
D-ATACOM
Learned / Learnable
Known
Safe Exploration /
Policy Learning
Safety Critic
Unknown
Safe Policy Learning
Value-Based Safety Critic
$$ V^{\pi}_{F}(s, \textcolor{orange}{a}) = \mathbb{E}_{\pi} \left[ \sum_{t} \gamma^t k(s_t) | s, \textcolor{orange}{a} \right] < \eta $$
- State-action value function eliminates the requirement for dynamic models
- Need to tune the threshold for different tasks
- Multiple constraints of different scales will not be treated equally
- Safety at each state can be non-deterministic due to partial observability or disturbances
Value-Based Safety Critic
$$ V^{\pi}_{F}(s, \textcolor{orange}{a}) = \mathbb{E}_{\pi} \left[ \sum_{t} \gamma^t k(s_t) | s, \textcolor{orange}{a} \right] < \eta $$
- State-action value function eliminates the requirement for dynamic models
- Need to tune the threshold for different tasks
- Multiple constraints of different scales will not be treated equally
- Safety at each state can be non-deterministic due to partial observability or disturbances
Safe Probability Function
Safe probability of a state $p_b(s)$
For a trajectory $\tau$, the safe probability is
$p(c=1|\tau) = \prod\limits_{t=0}^{\infty} p_b(s_t)$
Discount factor $\gamma$ as termination probablity of a state
Trajectory of horizon $h$ has the probablity
$ p^{H}(h)=(1-\gamma)\prod_{t=0}^{h-1}\gamma$
Safe Probability Function of finite horizon
$$ p(c^{\pi}=1|s, a) = \sum_{h=0}^{\infty} p^{H}(h) \mathbb{E}_{\tau_h \sim \pi} \left[ \prod_{t=0}^{h}p_b(s_t) | s, a \right]$$
Value-Based Safety Critic
$$ V^{\pi}_{F}(s, a) = \mathbb{E}_{\pi} \left[ \sum_{t} \gamma^t k(s_t) | s, a \right] < \eta $$
- State-action value function eliminates the requirement for dynamic models
- Need to tune the threshold for different tasks
- Multiple constraints of different scales will not be treated equally
- Safety at each state can be non-deterministic due to partial observability or disturbances
Safe Probability Function
Safe Probability Function of finite horizon
$$ p(c^{\pi}=1|s, a) = \sum_{h=0}^{\infty} p^{H}(h) \mathbb{E}_{\tau_h \sim \pi} \left[ \prod_{t=0}^{h}p_b(s_t) | s, a \right]$$

Safe Probability Bellman Equation
$$ p(c^{\pi}=1|s, a) = \sum_{h=0}^{\infty} p^{H}(h) \mathbb{E}_{\tau_h \sim \pi} \left[ \prod_{t=0}^{h}p_b(s_t) | s, a \right]$$
Let $\psi^{\pi}(s, a) \coloneqq p(c^{\pi}=1|s, a)$, we get
$ \psi^{\pi}(s, a) = $ $\underbrace{(1 - \gamma) p_b(s)}_{\text{safe absorbing}}$ + $\underbrace{\gamma p_b(s) \mathbb{E}_{s', a' \sim \pi } \left[\psi^{\pi}(s', a')\right]}_{\text{safe non-absorbing}}$
Further Extensions
- Model estimation could be wrong for out-of-distribution data point
Prior Network and Knowledge Uncertainty
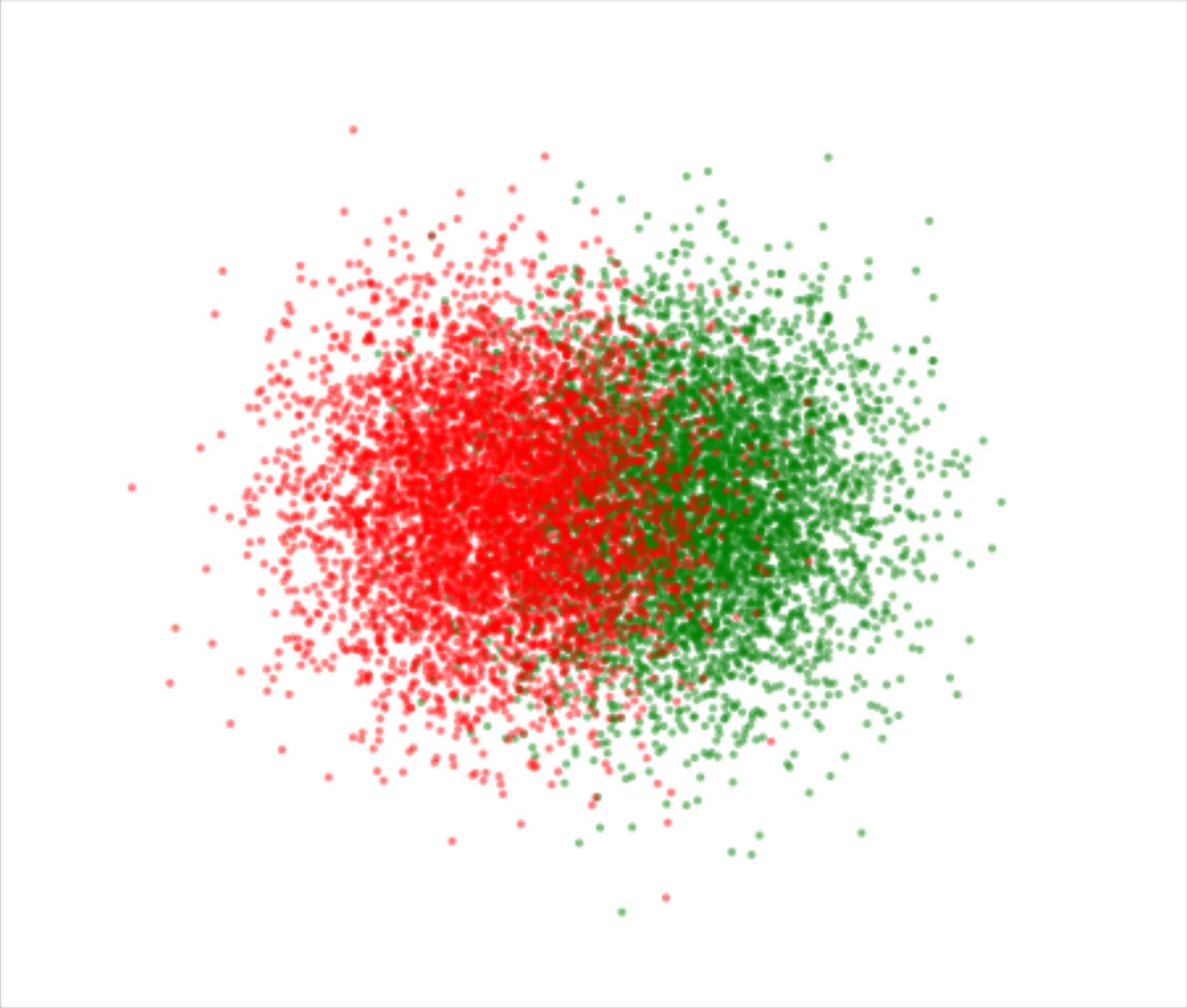
Dataset

Classification
Uncertainty Quantification
- Aleatoric Uncertainty - Data Uncertainty
- Epistemic Uncertainty - Model Uncertainty / Knowledge Uncertainty
Prior Network [Manilin et al, (2018, 2019)]
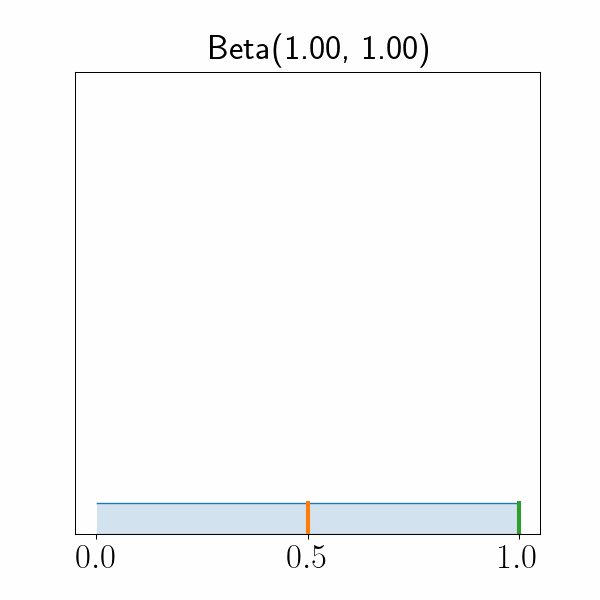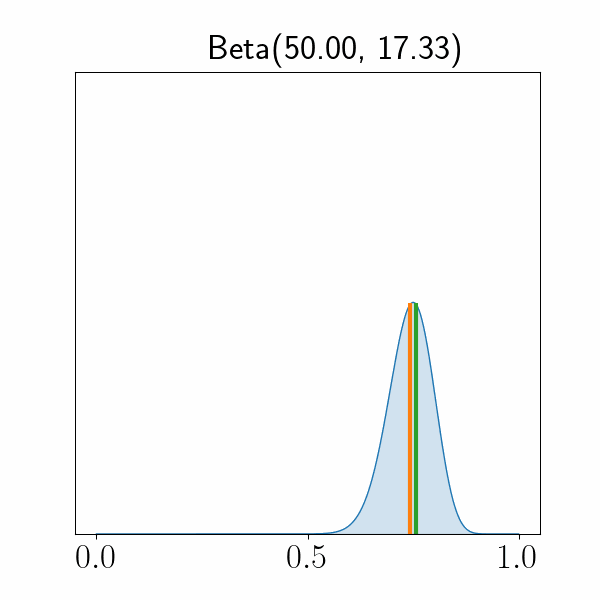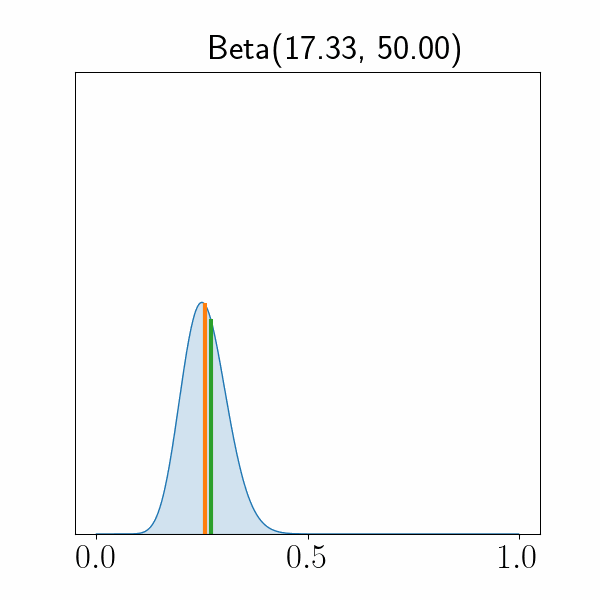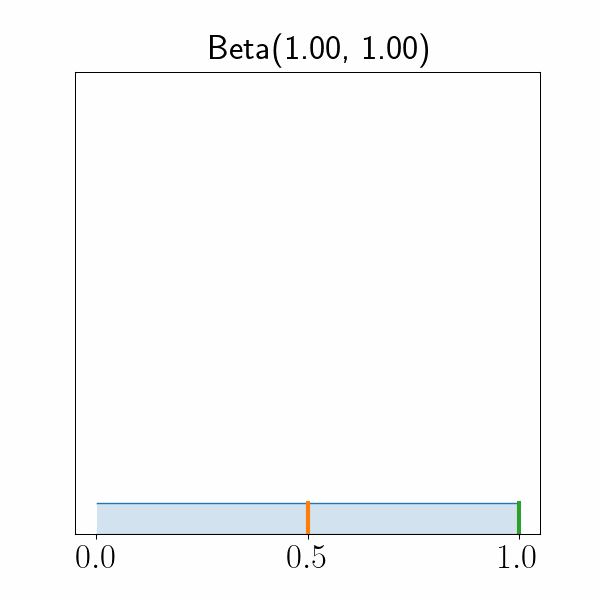
$p(\psi|x) = \text{Beta}(\psi; \alpha_1(x), \alpha_2(x))$

Dataset

Classification
Uncertainty Quantification
- Aleatoric Uncertainty - Data Uncertainty
- Epistemic Uncertainty - Model Uncertainty / Knowledge Uncertainty
Prior Network [Manilin et al, (2018, 2019)]
$p(\psi|x) = \text{Beta}(\psi; \alpha_1(x), \alpha_2(x))$
Uncertainty Quantification
- Aleatoric Uncertainty - Data Uncertainty
- Epistemic Uncertainty - Model Uncertainty / Knowledge Uncertainty
Prior Network [Manilin et al, (2018, 2019)]
$p(\psi|x) = \text{Beta}(\psi; \alpha_1(x), \alpha_2(x))$
Prior Network for Binary Classification
$$ p(c|x;\mathcal{D}) = \iint \underbrace{p(c|\psi)}_{\text{Data}} \underbrace{p(\psi|x; \theta)}_{\text{Knowledge}} \underbrace{p(\theta|\mathcal{D})}_{\text{Model}} \mathrm{d}\psi \mathrm{d}\theta $$
Knowledge Uncertainty
$$ U(x) = \mathcal{MI}(c, \psi|x; \mathcal{D}) $$

Dataset

Prediction

Total Uncertainty

Knowledge Uncertainty
Safe Upper Knowledge Bound
- Safe Upper Knowledge Bound (SUKB) $$\mathcal{K}_{\zeta}(s, a) = \textcolor{orange}{p(c^{\pi}=1|s, a)} + \zeta U(s, a)$$
- Predictive Mean of uniform distribution leads to conservative behavior
- Keep exploration for unknown state action pair
- Safe Upper Knowledge Bound (SUKB) $$\mathcal{K}_{\zeta}(s, a) = \textcolor{orange}{p(c^{\pi}=1|s, a)} + \zeta U(s, a)$$
- Predictive Mean of uniform distribution leads to conservative behavior
- Keep exploration for unknown state action pair
Safe Policy Learning
$$ \max_{\pi} \quad Q^{\pi}(s, a) \quad \quad \text{s.t.} \quad \textcolor{#bd7ebe}{\mathcal{K}^{\pi}_{\zeta}(s, a)} > \eta $$
Policy Learning as Inference
$\min_{\pi} \quad \text{KL}\left[ \pi(a|s) \left\Vert p^{\pi}_{\text{safe}}(a|s)\right.\right] $
Optimal Distribution
$ \textcolor{#87bc45}{p^{\pi}_{Q}(s, a) = \frac{1}{Z_Q} \exp\left( \beta_q Q^{\pi}(s, a) \right)} $
Safe Distribution
$ \textcolor{#7eb0d5}{p^{\pi}_{\mathcal{K}}(s, a) = \frac{1}{Z_k} \exp\left( \beta_k [\mathcal{K}_\zeta^{\pi}(s, a) - \eta]_{-}^2 \right)}$
Safe Optimal Distribution
$ \textcolor{#fd7f6f}{p^{\pi}_{\text{safe}}(a|s) \propto p^{\pi}_{Q}(s, a) p^{\pi}_{\mathcal{K}}(s, a)} $
Experiments
ATACOM

ATACOM exploits the knowledge of constraints and dynamics to enable robots to explore safely in the real world
Safe Exploration
Chapter 2
ReDSDF / D-ATACOM

Pre-trained ReDSDF serve as constraint for collision avoidance.
D-ATACOM handles long-term safety during training
Safe Exploration / Policy Learning
Chapter 3
SPF / DSPF


SPF/DSPF provide a dimensionless safety critic enables model-free safe policy learning considering knowledge uncertainty
Safe Policy Learning
Chapter 4
Air Hockey Challenge
Robot Air Hockey Challenge 2025
Final event at IROS in Hangzhou
Kinodynamic Neural Planner
Trick Hitting
Dynamic Hitting
Backup Slides
ATACOM - Extensions
$\begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix} = \textcolor{b2e061}{\underbrace{-\mJ_u^{\dagger} \vpsi}_{\text{Drift Comp.}}}$ $\textcolor{#fd7f6f}{\underbrace{- \lambda \mJ_u^{\dagger} \vc}_{\text{ Contraction }}}$ $\textcolor{7eb0d5}{\underbrace{+ \mB_u \va }_{\text{ Tangential }}} $
| Problem | State | Constraint $\vc=0$ | Dynamics | Jacobian $ \mJ_u$ | Drift $\vpsi$ |
|---|---|---|---|---|---|
| ATACOM | $\vs$ | $k(\vs) + \vmu$ | $f(\vs) + G(\vs) \vu_s$ | $\begin{bmatrix} \mJ_k \mG & A \end{bmatrix}$ | $\mJ_k \vf$ |
| Second Order | $\begin{bmatrix} \vs \\ \dot{\vs} \end{bmatrix}$ | $\zeta(k(\vs)) + \mJ_k(\vs) \dot{\vs} + \vmu$ | $\begin{bmatrix} \vzero \\ f(\vs, \dot{\vs}) \end{bmatrix} + \begin{bmatrix} \vzero \\ G(\vs, \dot{\vs}) \end{bmatrix} \vu_s $ | $\begin{bmatrix} \mJ_k \mG & A \end{bmatrix}$ | $\mJ_k \vf + (\mJ_{\zeta}\mJ_k + \nabla_s\mJ_k \dot{\vs}) \dot{\vs}$ |
| Dynamic Env. | $\begin{bmatrix} \vq \\ \vz \end{bmatrix}$ | $k(\vq, \vz) + \vmu$ | $f(\vq) + G(\vq) \vu_q$ | $\begin{bmatrix} \mJ_q \mG & A \end{bmatrix}$ | $\mJ_q \vf + \mJ_z\dot{\vz}$ |
| Equality Constraint | $\vs$ | $\begin{bmatrix} k(\vs) + \vmu \\ l(\vs) \end{bmatrix}$ | $f(\vs) + G(\vs) \vu_s$ | $\begin{bmatrix} \mJ_k \mG & A \\ \mJ_l \mG & \vzero \end{bmatrix}$ | $\begin{bmatrix} \mJ_k \vf \\ \mJ_l \vf \end{bmatrix}$ |
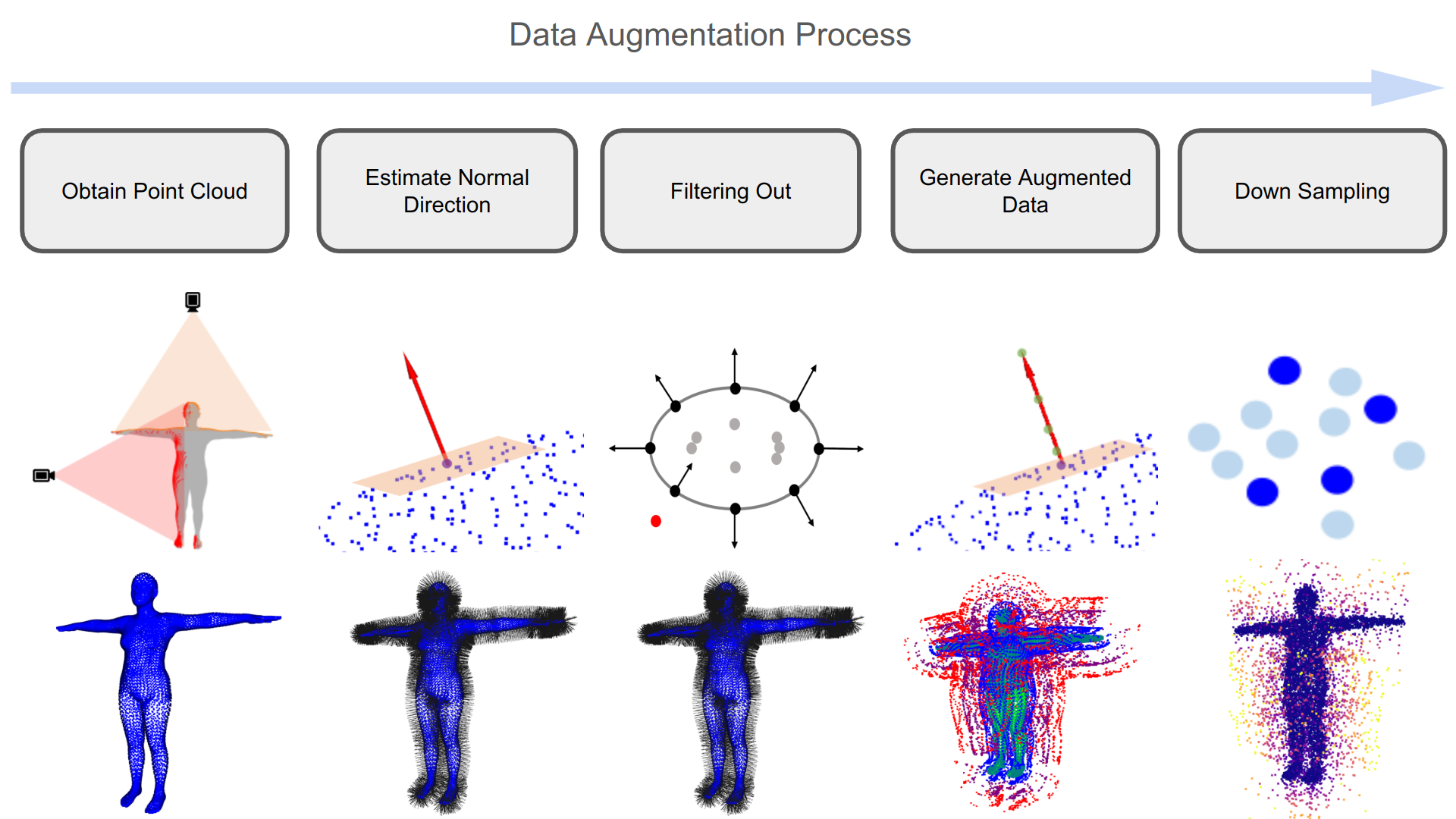
ReDSDF - Data Augmentation and Training
$$ d_{\theta}(\vx, \textcolor{DarkSalmon}{\vq}) = \left[1-\sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\right]\textcolor{LightGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\textcolor{Orange}{ \underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
$ \sigma_{\vtheta}(\vx, \vq) = \sigmoid\left(\textcolor{OrangeRed}{\alpha_{\vtheta}}\left( \lVert\vx - \vx_c\rVert_2 - \textcolor{OrangeRed}{\rho_{\vtheta}} \right)\right) $
$$ \mathcal{L} = \sum \left[ \Vert d_{q,x} - d_{\theta}(q, x) \Vert^2 + \Vert \mathrm{null}(\nabla_{x}d_{\theta}(\vq, \vx)) \vn_{q, x} \Vert^2 + \Vert \nabla_{x}d_{\theta}(\vq, \vx) \mathrm{null}(\vn_{q, x}) \Vert^2 + \gamma \rho_{\theta}^2(\vq, \vx) \right] $$
Theoretical Analysis

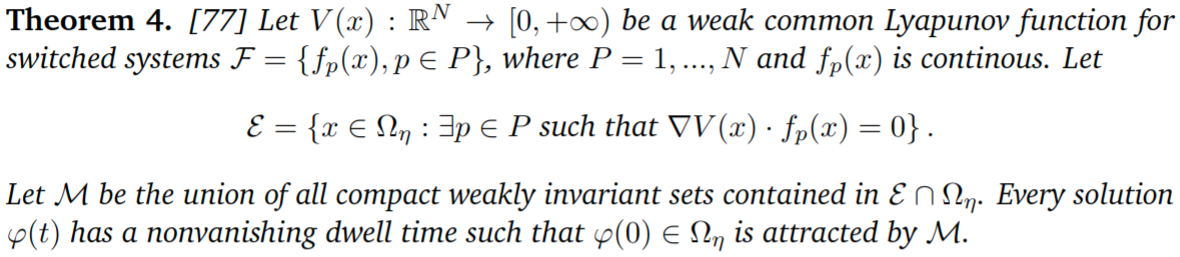

Theoretical Analysis

Backup - Smooth Tangent Space Basis
Safe Variable Function
Random variable of state being safe $$C_s \sim \mathrm{Be}(c; p_b(s))$$
Safe Variable Function under policy $\pi$
$$ C^{\pi}(s) = \prod_{t=0}^{\infty}C_t, \quad S_0=s$$
Random variable of state is non-absorbing $$ Y_t \sim \mathrm{Be}(y; \gamma) $$
Trajectory of horizon h is $$\mathbb{1}(H=h) = (1-Y_h)\prod_{t=0}^{h-1}Y_t$$
Safe Probability Bellman Equation
$$ C^{\pi}(s) = \textcolor{orange}{\sum_{h=0}^{\infty} (1-Y_h) \prod_{t=0}^{h-1} Y_t} \prod_{t=0}^{\textcolor{orange}{h}}C_t, \quad S_0=s$$
Safe Variable Bellman Equation
$C^{\pi}(s)$ $= \underbrace{(1-Y_0)C_s \vphantom{\sum_{h=1}^{\infty}} }_{h=0} + \underbrace{Y_0 C_s \sum_{h=1}^{\infty} (1-Y_h)\prod_{t=1}^{h-1} Y_t \prod_{t=1}^{h}C_t}_{h\geq1}$
$\stackrel{\mathcal{D}}{=} (1-Y_0)C_s + Y_0 C_s C^{\pi}(S')$ $\quad\quad\quad\quad\;$
Safe Variable Bellman Equation
$C^{\pi}(s)$ $\phantom{= \underbrace{(1-Y_0)C_s \vphantom{\sum_{h=1}^{\infty}} }_{h=0} + \underbrace{Y_0 C_s \sum_{h=1}^{\infty} (1-Y_h)\prod_{t=1}^{h-1} Y_t \prod_{t=1}^{h}C_t}_{h\geq1}}$
$\stackrel{\mathcal{D}}{=} (1-Y_0)C_s + Y_0 C_s C^{\pi}(S')\quad\quad\quad\quad\;$
Let $\Psi^{\pi}(s) \coloneqq p(C^{\pi}=1|s)$ and $\widehat{\Psi}^{\pi}(s) \coloneqq p(C^{\pi}=0|s)$, we get the Safe Probablity Bellman Equation
$$ \begin{split} \psi^{\pi}(s, \textcolor{orange}{a}) &= \underbrace{(1 - \gamma) p_b(s)}_{\text{safe absorbing}} + \underbrace{\gamma p_b(s) \mathbb{E}_{s', \textcolor{orange}{a'}}\left[\Psi^{\pi}(s', \textcolor{orange}{a'})\right]}_{\text{safe non-absorbing}} \\ \widehat{\Psi}^{\pi}(s, \textcolor{orange}{a}) &= \underbrace{1 - p_b(s) \vphantom{\left[\widehat{\psi}^{\pi}(s')\right]}}_{\text{unsafe}} + \underbrace{\gamma p_b(s) \mathbb{E}_{s', \textcolor{orange}{a'}}\left[\widehat{\Psi}^{\pi}(s', \textcolor{orange}{a'})\right]}_{\text{safe non-absorbing}} \end{split} $$
Uncertainty of ML model
- Aleatoric Uncertainty - Data Uncertainty
- Epistemic Uncertainty - Model Uncertainty / Knowledge Uncertainty
Conjugate Prior of Bernoulli Distribution $p(\psi|x) = \text{Beta}(\psi; \alpha_1(x), \alpha_2(x))$
Prior Network for Binary Classification
$$ p(c|x;\mathcal{D}) = \iint \underbrace{p(c|\psi)}_{\text{Data}} \underbrace{p(\psi|x; \theta)}_{\text{Knowledge}} \underbrace{p(\theta|\mathcal{D})}_{\text{Model}} \mathrm{d}\psi \mathrm{d}\theta $$
Knowledge Uncertainty
$$U(x) = \mathcal{MI}(c, \psi|x; \mathcal{D}) = \underbrace{\mathcal{H}\left[\mathbb{E}_{p(\psi|x;\mathcal{D})}[p(c|\psi)]\right]}_{\text{Total Uncertainty}} - \underbrace{\mathbb{E}_{p(\psi|x;\mathcal{D})}\left[ \mathcal{H}[p(c|\psi)]\right]}_{\text{Expected Data Uncertainty}} $$

Dataset

Prediction

Total Uncertainty

Knowledge Uncertainty
Distributional Safe Probability Bellman Equation
Safe Probablity Bellman Equation
$$ \psi^{\pi}(s, a) = (1 - \gamma) p_b(s) + \gamma p_b(s) \mathbb{E}_{s', a'}\left[\psi^{\pi}(s', a')\right]$$
Distributional Safe Probablity Bellman Equation
Consider $\Psi(s,a) \sim \text{Beta}(\psi|s, a)$
$$ \Psi(s, a) \stackrel{\mathcal{D}}{=} (1 - \gamma) p_b(s) + \gamma p_b(s) \mathbb{E}_{s', a'}\left[\Psi( s', a')\right] $$
Training Loss $\mathcal{L}_{\theta} = d(\Psi_{\theta}(s, a), \Psi_{\text{T}}(s, a))$