Safe and Reliable Robot Reinforcement Learning in Dynamic Environments
Puze Liu
Techinal University Darmstadt
Motivation


Atari and Go, DeepMind


Atari and Go, DeepMind
Dexterous Manipulation, OpenAI
Locomotion, ETH
How to build safe and reliable reinforcement learning algorithms for robotic system?
Challenges in safe robot reinforcement learning
- Physical interaction
- Dynamical environment
- Imperfect simulation
- High costs for reparing
- Disturbances and noise
- Problem formulation
Safety Constraints in Safe Reinforcement Learning
Cumulative Cost
$$ \mathbb{E}_{\tau} \left[ \sum_{t=0}^{T} \gamma^{t} c(\vs_t, \va_t) \right] \leq 0 $$
- Does not require an explicit form
- Deals with trajectory level constraints
- No safety guarantee in exploration process
- Requires good simulation
Cumulative Cost
$$ \mathbb{E}_{\tau} \left[ \sum_{t=0}^{T} \gamma^{t} c(\vs_t, \va_t) \right] \leq 0 $$
- Does not require an explicit form
- Deals with trajectory level constraints
- No safety guarantee in exploration process
- Requires good simulation
(Conditional) Value at Risk
$$ \mathrm{Pr}\left(c(\vs_t, \va_t) < 0 \right) \geq \eta $$
- Considers noises and disturbances
- Robust solution
- Gaussian assumption or sampling-based
- Conservative policy
Cumulative Cost
$$ \mathbb{E}_{\tau} \left[ \sum_{t=0}^{T} \gamma^{t} c(\vs_t, \va_t) \right] \leq 0 $$- Does not require an explicit form
- Deals with trajectory level constraints
- No safety guarantee in exploration process
- Requires good simulation
(Conditional) Value at Risk
$$ \mathrm{Pr}\left(c(\vs_t, \va_t) < 0 \right) \geq \eta $$
- Considers noises and disturbances
- Robust solution
- Gaussian assumption or sampling-based
- Conservative policy
Hard Constraint
$$ c(\vs_t, \va_t) < 0 $$
- Guarantees safety during exploration
- Enables Learning in the real world
- Requires prior knowledge
Problem Formulation
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & c(\vs_t) < 0 \end{align*}$$ with $\vs_t \in \RR^{S}$ and $c:\RR^{S}\rightarrow \RR^{N}$
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & c(\vs_t) < 0 \end{align*}$$ with $\vs_t \in \RR^{S}$ and $c:\RR^{S}\rightarrow \RR^{N}$
Core Idea
Construct a Constrained Manifold and a corresponding Action Space that enables control actions to move states along the Tangent Space of the constrained manifold.
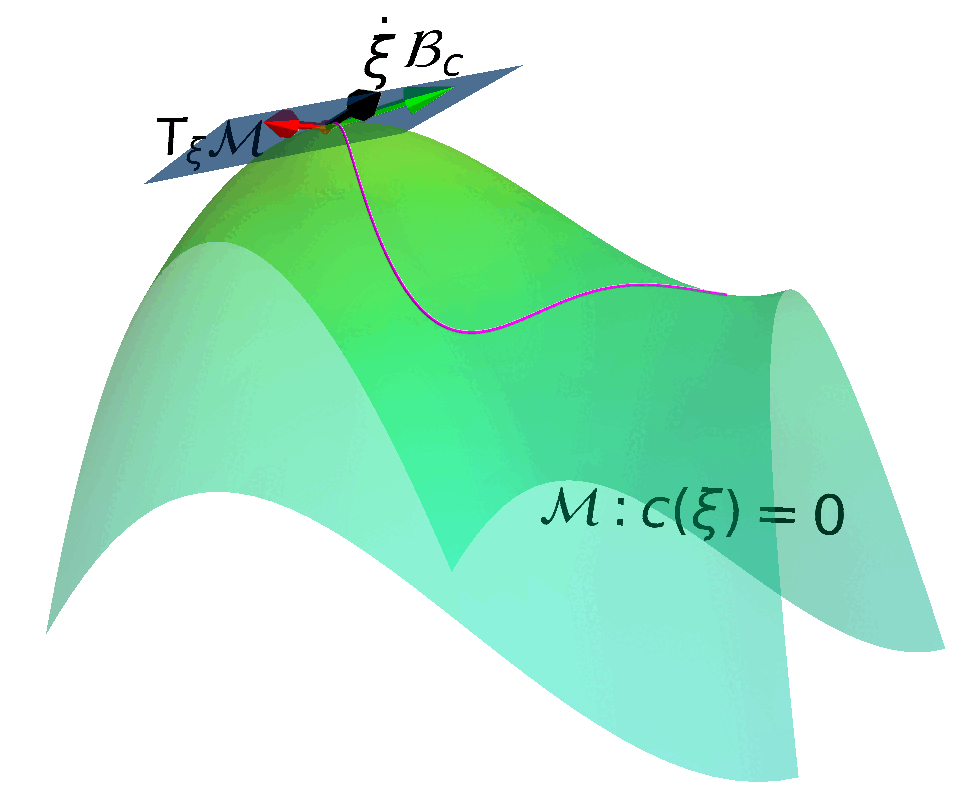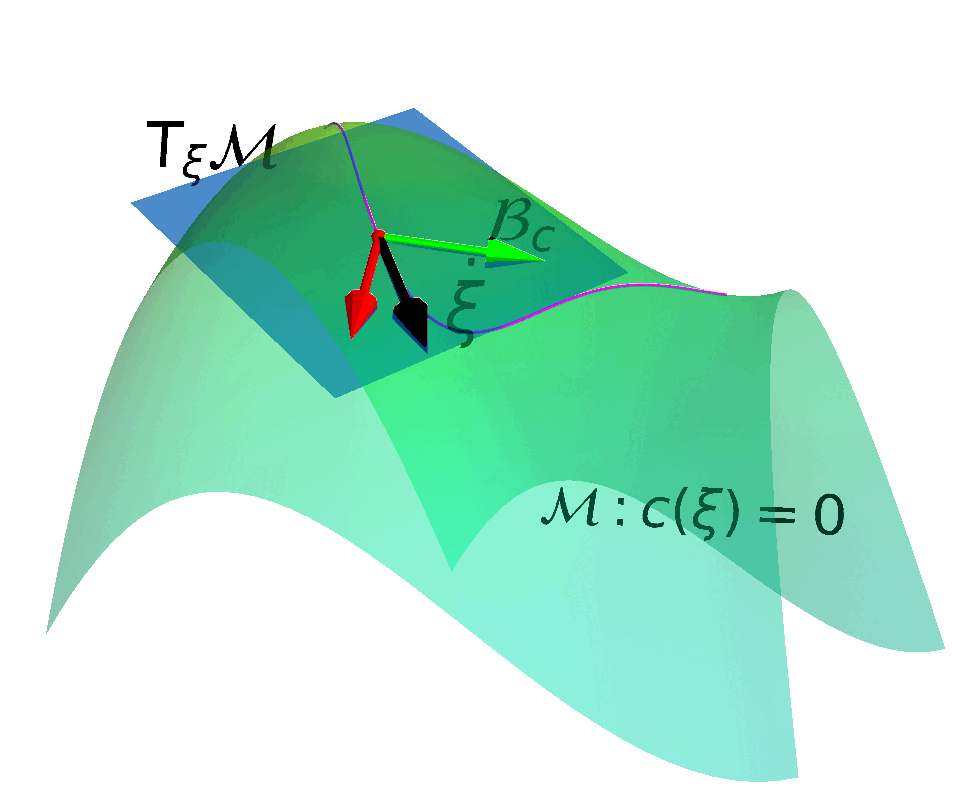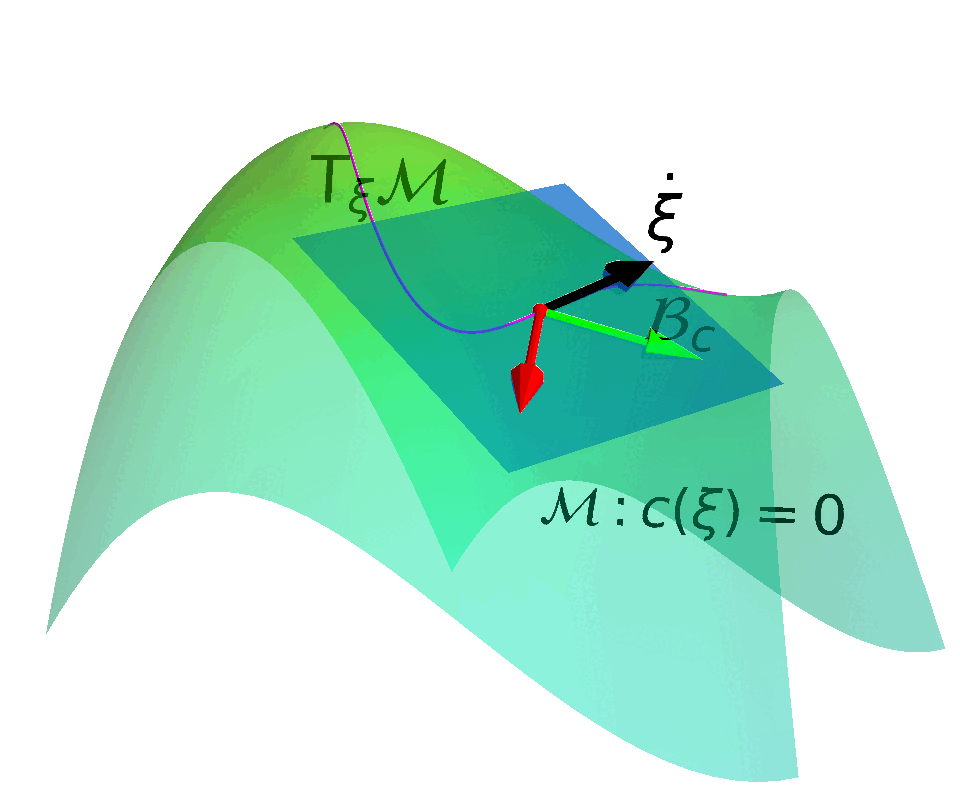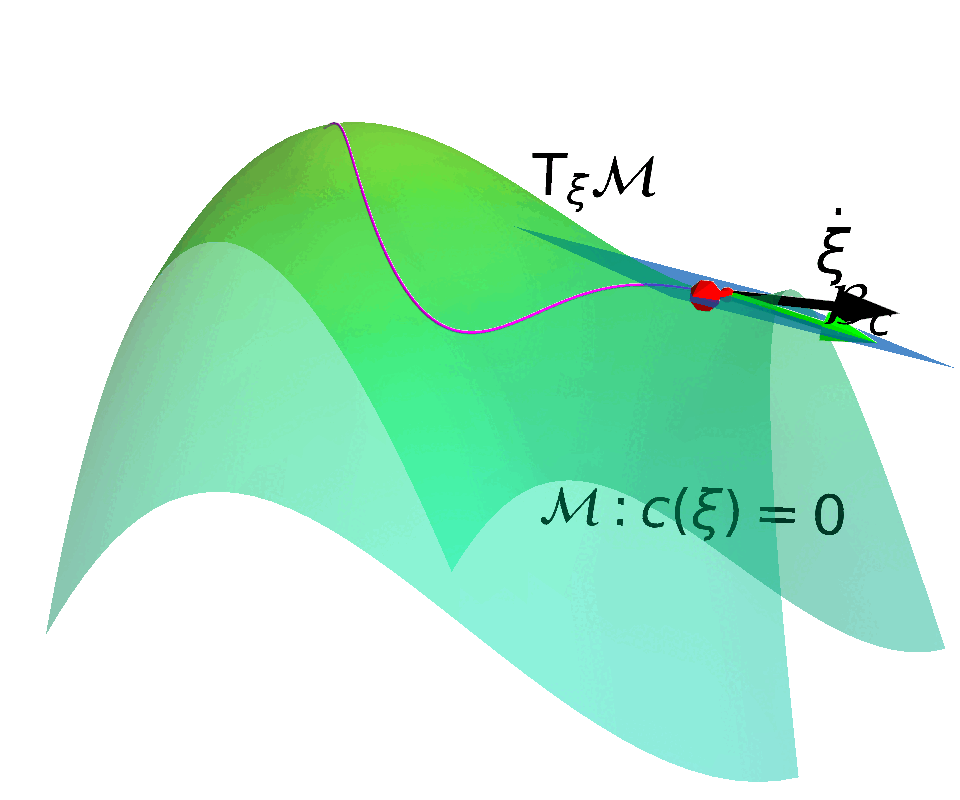
Embedded Manifold
$$ \MM = \{ \vxi \in \RR^N: f(\vxi) = 0\}$$
with $f:\RR^N \rightarrow \RR^M$ being smooth. $\MM$ is a $R$-dimensional submanifold embedded in $\RR^N$ if $f$ has a constant rank $R \leq \min(N, M)$.
$$ \MM = \{ \vxi \in \RR^N: f(\vxi) = 0\}$$
with $f:\RR^N \rightarrow \RR^M$ being smooth. $\MM$ is a $R$-dimensional submanifold embedded in $\RR^N$ if $f$ has a constant rank $R \leq \min(N, M)$.
$$ \mathcal{M} = \{ (x_1, x_2) \in \RR^2: x_1 ^ 2 + x_2^2 - 1= 0 \}$$
$$ \mJ = \begin{bmatrix} 2x_1 & 2 x_2 \end{bmatrix} $$

1D manifold embedded in $\RR^2$
$$ \MM = \{ \vxi \in \RR^N: f(\vxi) = 0\}$$
with $f:\RR^N \rightarrow \RR^M$ being smooth. $\MM$ is a $R$-dimensional submanifold embedded in $\RR^N$ if $f$ has a constant rank $R \leq \min(N, M)$.
$$ \mathcal{M} = \{ (x_1, x_2) \in \RR^2: x_1 ^ 2 + x_2^2 - 1= 0 \}$$
$$ \mJ = \begin{bmatrix} 2x_1 & 2 x_2 \end{bmatrix} $$

1D manifold embedded in $\RR^2$
$$ \mathcal{M} = \{ (x_1, x_2) \in \RR^2: x_1 ^ 2 - x_2^4 = 0 \}$$
$$ \mJ = \begin{bmatrix} 2x_1 & -3 x_2^3 \end{bmatrix} $$

Not a Manifold
Constraint Manifold
$c(\vs) < 0$, $c: \RR^S \rightarrow \RR^N$
$c(\vs) < 0$, $c: \RR^S \rightarrow \RR^N$
We introduce a slack variable $\vmu \in \RR^N$
$\MM = \left \{(\vs, \vmu)\in \RR^{S+N}: \tilde{c}(\vs, \vmu) : = c(\vs) + h(\vmu) = \vzero \right \} $
with $h(\vmu)=\begin{bmatrix} h_1(\mu_1) \\ \cdots \\ h_N(\mu_N) \end{bmatrix}$, $h_i:\RR \rightarrow \RR^+$
The Jacobian is $$ J_c(\vs, \vmu) = \begin{bmatrix} c'(\vs) & h'(\vmu) \end{bmatrix}$$
$c(\vs) < 0$, $c: \RR^S \rightarrow \RR^N$
We introduce a slack variable $\vmu \in \RR^N$
$\MM = \left \{(\vs, \vmu)\in \RR^{S+N}: \tilde{c}(\vs, \vmu) := c(\vs) + h(\vmu) = \vzero \right \} $
with $h(\vmu)=\begin{bmatrix} h_1(\mu_1) \\ \cdots \\ h_N(\mu_N) \end{bmatrix}$, $h_i:\RR \rightarrow \RR^+$
The Jacobian is $$ J_c(\vs, \vmu) = \begin{bmatrix} c'(\vs) & h'(\vmu) \end{bmatrix}$$
Example
$ s < 0 $
$ \Rightarrow s + \exp(\mu)=0 $
$\mJ = \begin{bmatrix} 1 & \exp(\mu) \end{bmatrix}$
Constraint Manifold: Examples
Constraint: $ x_1^2 + x_2^2 < 1 $
$$ \MM = \{(x_1, x_2, \mu) \in \RR^3: x_1^2 + x_2^2 + \exp(\mu) - 1 = 0 \} $$
$$J_c(x_1, x_2, \mu) = \begin{bmatrix} 2 x_1 & 2 x_2 & \exp(\mu) \end{bmatrix}$$
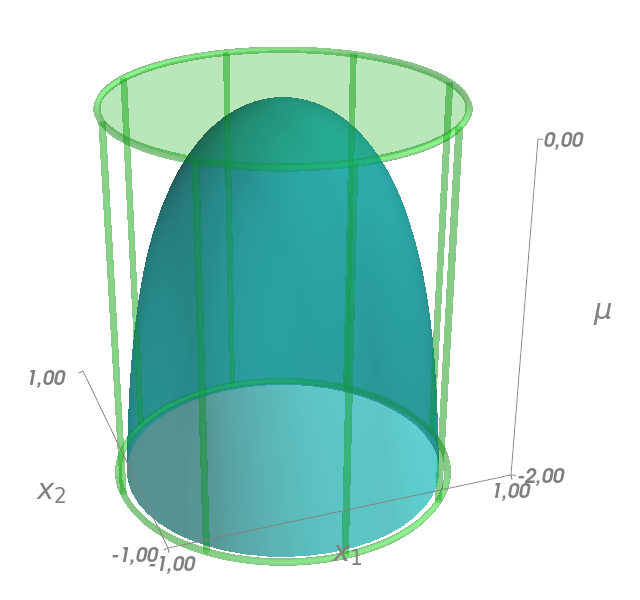
Constraint: $ x_1^2 + x_2^2 < 1 $
$$ \MM = \{(x_1, x_2, \mu) \in \RR^3: x_1^2 + x_2^2 + \exp(\mu) - 1 = 0 \} $$
$$J_c(x_1, x_2, \mu) = \begin{bmatrix} 2 x_1 & 2 x_2 & \exp(\mu) \end{bmatrix}$$

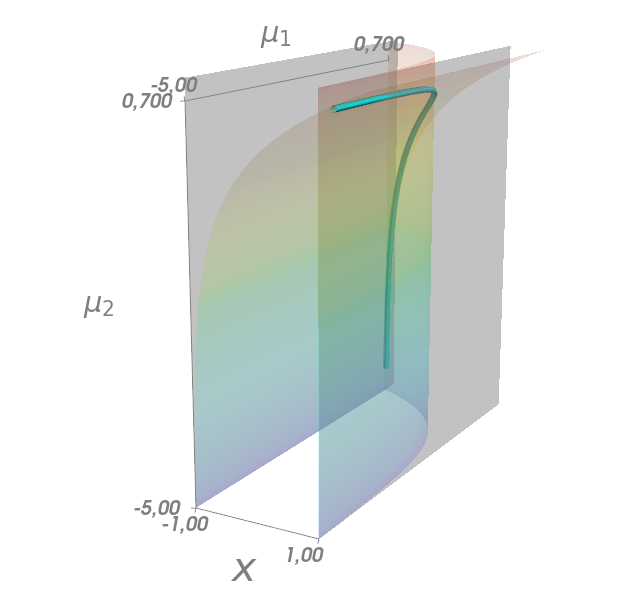
Constraints: $ -1 < x < 1 $
$$ \MM = \left\{(x, \mu_1, \mu_2) \in \RR^3: \begin{bmatrix} x + \exp(\mu_1) - 1 \\ -x + \exp(\mu_2) -1 \end{bmatrix} = \vzero \right\}$$
$$J_c(x, \mu_1, \mu_2) = \begin{bmatrix} 1 & \exp(\mu_1) & 0 \\ -1 & 0 & \exp(\mu_2)\end{bmatrix}$$
Tangent Space
$$ \mathrm{T}_{(s, \mu)} \MM = \left\{ \vv \in \RR^{S+N}: J_c(\vs, \vmu) \vv = 0 \right\}$$
$$ \mathrm{T}_{(s, \mu)} \MM = \left\{ \vv \in \RR^{S+N}: J_c(\vs, \vmu) \vv = 0 \right\}$$
The bases of the tangent space are
$$ \mathcal{B}_c(\vs, \vmu) = \begin{bmatrix} \vb_1 & ... & \vb_S \end{bmatrix} $$
with $\vb_i \in \mathrm{T}_{(s, \mu)}\MM $ such that $\mJ_c \bm{\mathcal{B}}_c = \vzero$.
$$ \mathrm{T}_{(s, \mu)} \MM = \left\{ \vv \in \RR^{S+N}: J_c(\vs, \vmu) \vv = 0 \right\}$$
The bases of the tangent space are
$$ \mathcal{B}_c(\vs, \vmu) = \begin{bmatrix} \vb_1 & ... & \vb_S \end{bmatrix} $$
with $\vb_i \in \mathrm{T}_{(s, \mu)}\MM $ such that $\mJ_c \bm{\mathcal{B}}_c = \vzero$.
The velocity in the tangent space is
$$ \dot{\vxi} = \begin{bmatrix}\dot{\vs} \\ \dot{\vmu} \end{bmatrix} = \mathcal{B}_c \va$$
We can also verify that $$\dot{\tilde{c}}(\vxi) = \mJ_c \dot{\vxi} = \mJ_c \mathcal{B}_c \va = \vzero$$

ATACOM Controller
Acting on the TAgent Space of the COnstraint Manifold
$$ \dot{\vxi} = \begin{bmatrix}\dot{\vs} \\ \dot{\vmu} \end{bmatrix} = \textcolor{#FF3E3E}{\underbrace{-\lambda \mJ_c^{\dagger}c(\vxi)}_{\text{Contraction Term}}} + \textcolor{cyan}{\underbrace{\mathcal{B}_c \va}_{\text{Propogation Term}}} $$

$$ \dot{\vxi} = \begin{bmatrix}\dot{\vs} \\ \dot{\vmu} \end{bmatrix} = \textcolor{#FF3E3E}{\underbrace{-\lambda \mJ_c^{\dagger}c(\vxi)}_{\text{Contraction Term}}} + \textcolor{cyan}{\underbrace{\mathcal{B}_c \va}_{\text{Propogation Term}}} $$
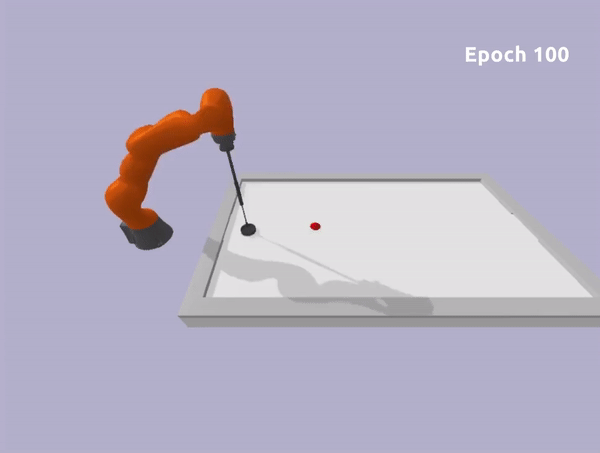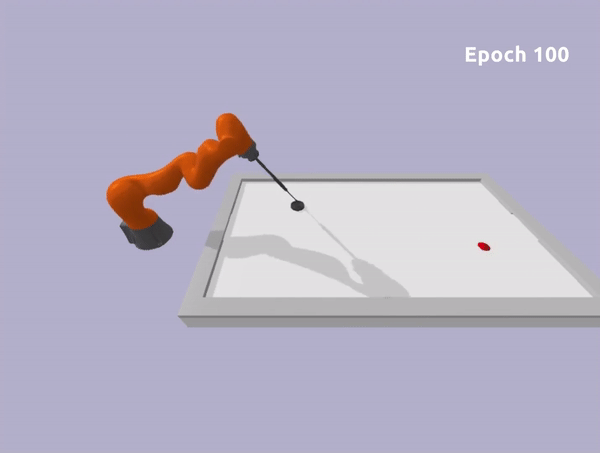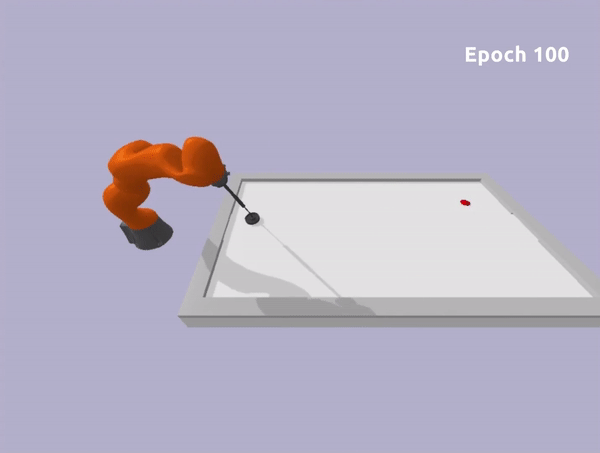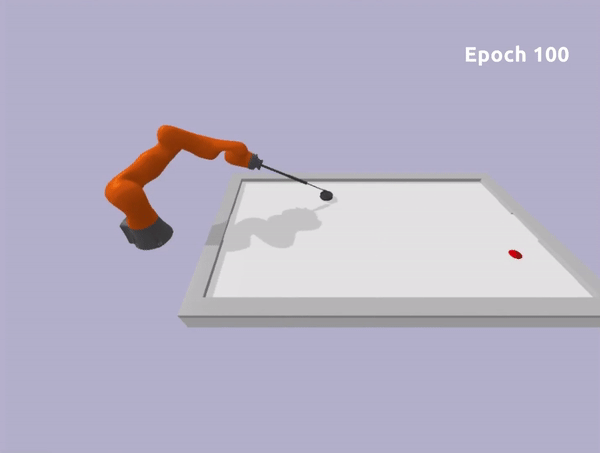
Toy Task
Epoch 0
Epoch 100

Experiments in Robotic Environment


Limitations
Extensions
1. Separable State Space
$$ \vs = \begin{bmatrix}\vq \\ \vx \end{bmatrix} $$ with $\vq_t \in \RR^{Q}$ and $\vx_t \in \RR^{X}$, $S = Q + X$
2. Control Affine System
$$ \dot{\vq} = f(\vq) + G(\vq) \vu $$
Modifications
1. Separable State Space
$$ \vs = \begin{bmatrix}\vq \\ \vx \end{bmatrix} $$ with $\vq_t \in \RR^{Q}$ and $\vx_t \in \RR^{X}$, $S = Q + X$
2. Control Affine System
$$ \dot{\vq} = f(\vq) + G(\vq) \vu $$
Constraint Manifold
$$ \MM = \{ (\vq, \vx, \vmu)\in \RR^{Q+X+N}: \tilde{c}(\vq, \vx, \vmu) = \vzero \} $$
with $\tilde{c}(\vq, \vx, \vmu) := c(\vq, \vx) + h(\vmu)$.
Constraint Manifold
$$ \MM = \{ (\vq, \vx, \vmu)\in \RR^{Q+X+N}: \tilde{c}(\vq, \vx, \vmu) = \vzero \} $$
with $\tilde{c}(\vq, \vx, \vmu) := c(\vq, \vx) + h(\vmu)$.
We can compute the time derivative $$\begin{align*}\dot{\tilde{c}}(\vq, \vx, \vmu) &= J_x(\vq, \vx) \dot{\vx} + J_q(\vq, \vx) \dot{\vq} + J_{\mu}(\vmu) \dot{\vmu} \\ \end{align*}$$
and substitute $\dot{\vq}$ with the control affine system $\dot{\vq} = f(\vq) + G(\vq) \vu$
$$\begin{align*}\dot{\tilde{c}}(\vq, \vx, \vmu) &= \textcolor{orange}{J_x(\vq, \vx) \dot{\vx} + J_q(\vq, \vx) f(\vq)} + \textcolor{yellowgreen}{J_q(\vq, \vx)G(\vq)}\vu + \textcolor{yellowgreen}{J_{\mu}(\vmu)} \dot{\vmu} \\ &= \textcolor{orange}{\Psi(\vq, \vx, \dot{\vx})} + \textcolor{yellowgreen}{J_c(\vq, \vx, \vmu)} \begin{bmatrix} \vu \\ \dot{\vmu} \end{bmatrix} \end{align*}$$
ATACOM Controller
Solve the equation
$$\begin{align*}\dot{\tilde{c}}(\vq, \vx, \vmu) &= \textcolor{orange}{\Psi(\vq, \vx, \dot{\vx})} + \textcolor{yellowgreen}{J_c(\vq, \vx, \vmu)} \begin{bmatrix} \vu \\ \dot{\vmu} \end{bmatrix} \end{align*} = \vzero$$
ATACOM Controller in general form
$$ \begin{bmatrix} \vu \\ \dot{\vmu} \end{bmatrix} = \underbrace{-\mJ_c^{\dagger} \Psi(\vq, \vx, \dot{\vx})}_{\text{Drift Compensation Term}} \underbrace{- \lambda \mJ_c^{\dagger} c(\vq, \vx, \vmu)}_{\text{Contraction Term}} \underbrace{+\mathcal{B}_c \va}_{\text{Propogation Term}}$$
ATACOM Controller in general form
$$ \begin{bmatrix} \vu \\ \dot{\vmu} \end{bmatrix} = \underbrace{-\mJ_c^{\dagger} \Psi(\vq, \vx, \dot{\vx})}_{\text{Drift Compensation Term}} \underbrace{- \lambda \mJ_c^{\dagger} c(\vq, \vx, \vmu)}_{\text{Contraction Term}} \underbrace{+\mathcal{B}_c \va}_{\text{Propogation Term}}$$
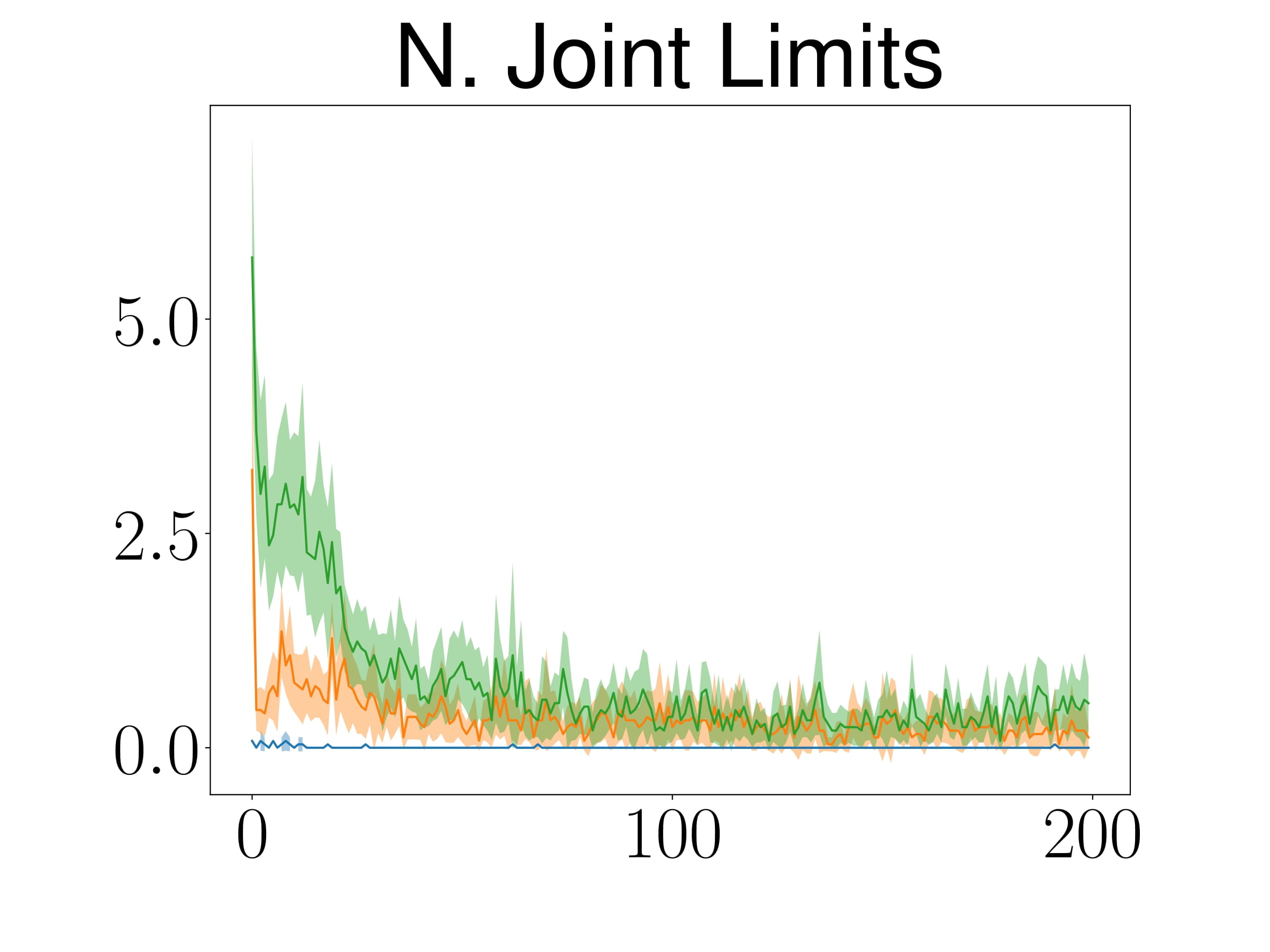
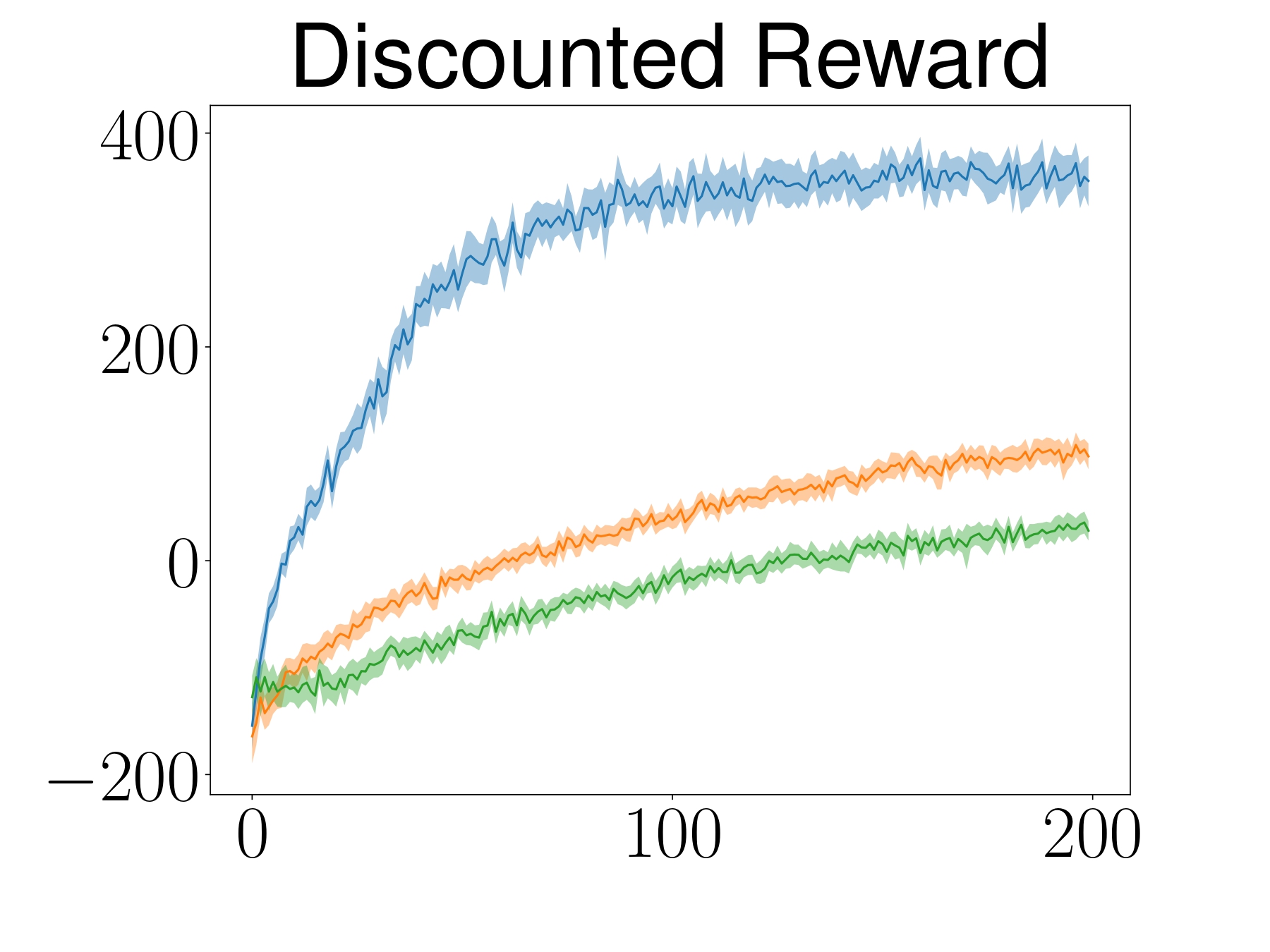
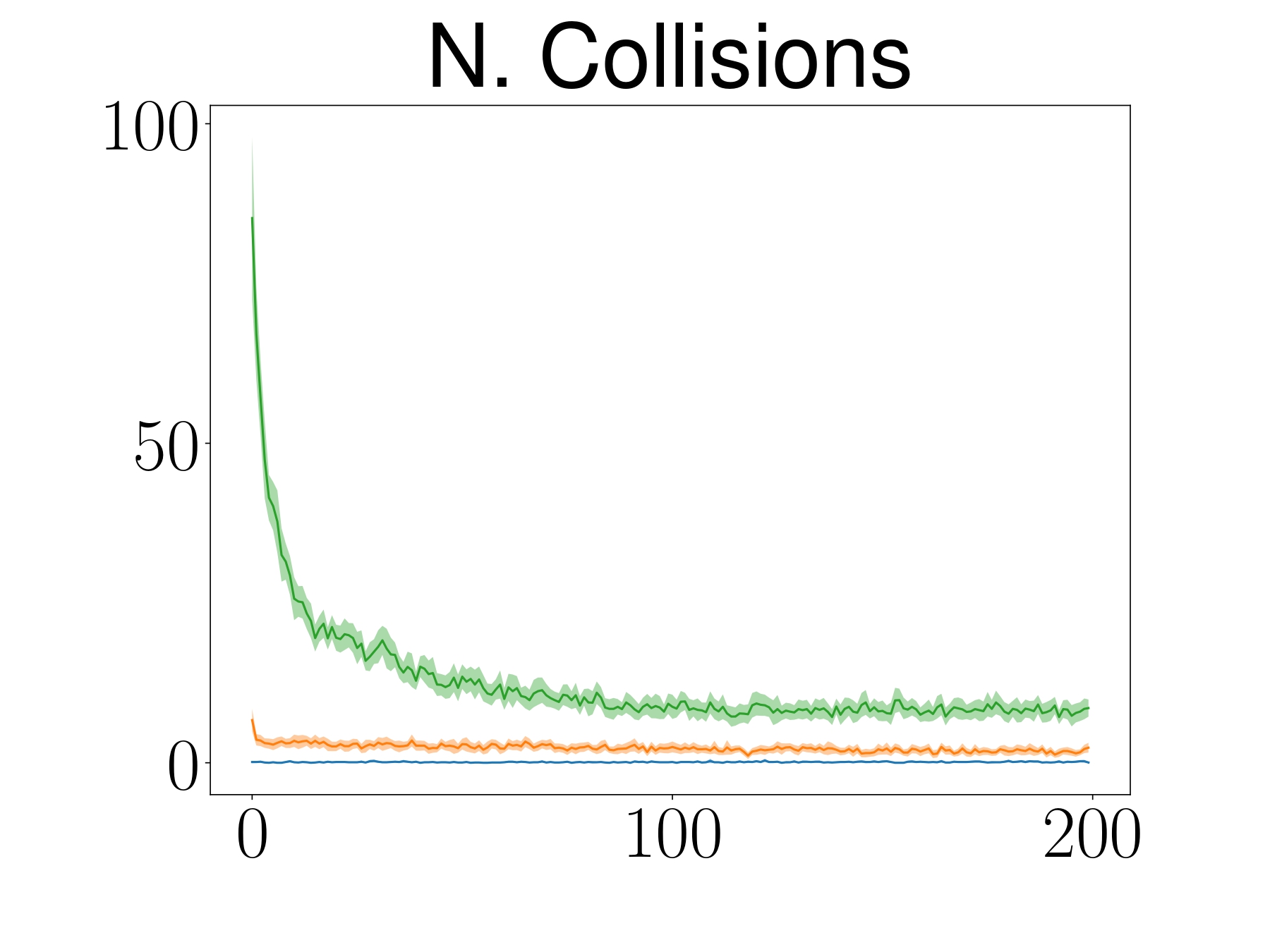
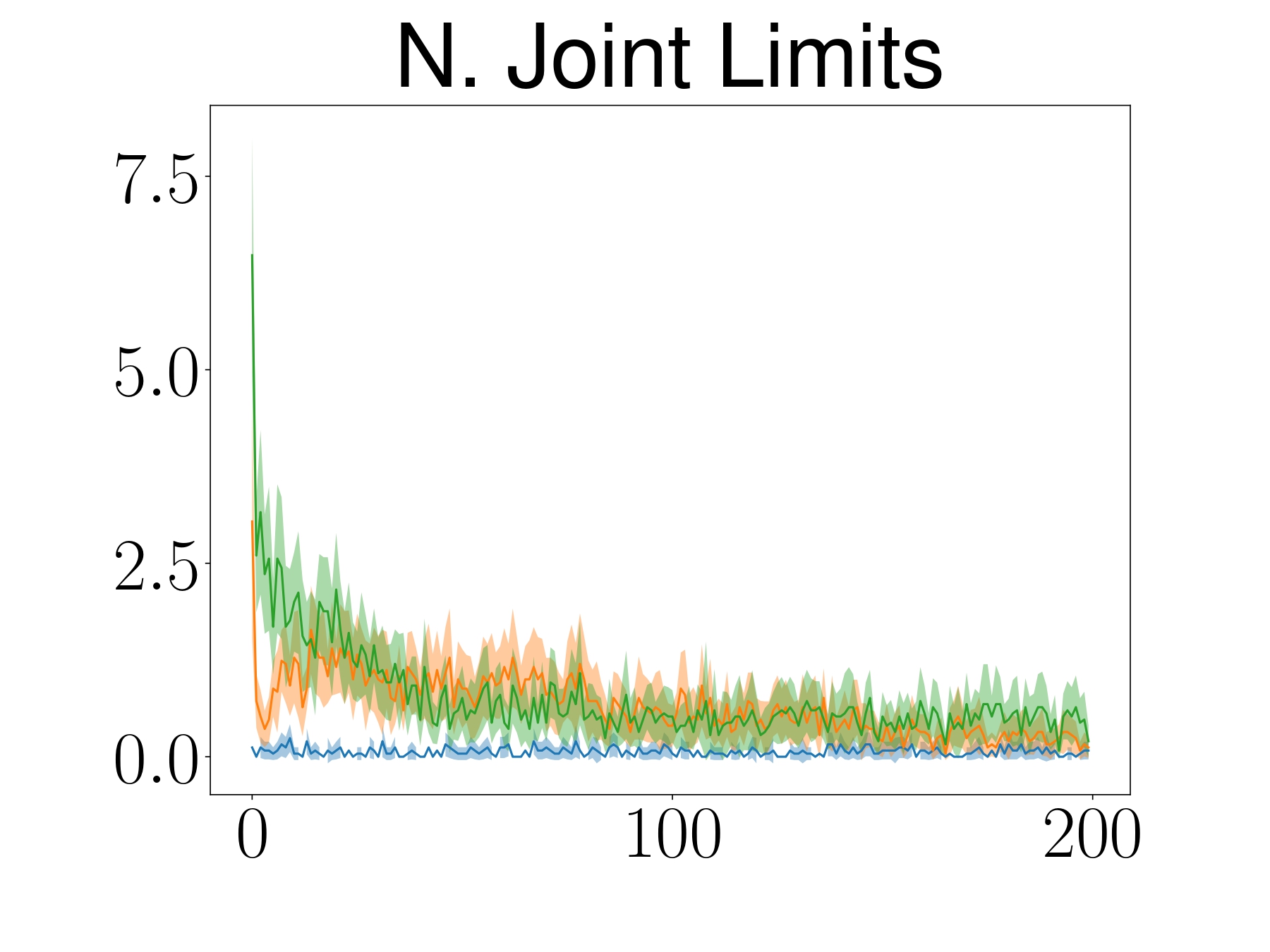
Safe Exploration in Dynamic Environment
- Stand-alone robot that moves blindly to the goal
- Differential drive as a control affine system
$$ \vq = \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} \quad f(\vq) = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \quad G(\vq) = \begin{bmatrix} \cos(\theta) & 0 \\ \sin(\theta) & 0 \\ 0 & 1 \end{bmatrix} \quad \va = \begin{bmatrix} v \\ \omega \end{bmatrix}$$
SAC
- Stand-alone robot that moves blindly to the goal
- Differential drive as a control affine system
$$ \vq = \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} \quad f(\vq) = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \quad G(\vq) = \begin{bmatrix} \cos(\theta) & 0 \\ \sin(\theta) & 0 \\ 0 & 1 \end{bmatrix} \quad \va = \begin{bmatrix} v \\ \omega \end{bmatrix}$$
SAC
ATACOM-SAC
How to design constraints?
- Task Dependent
- Expert Knowledge and Analysis
- First Attempt:
- Collision Avoidance
- Human-Robot-Interaction
- Dynamical Human Behavior
- Delicate and Reactive Manipulation


Collision Avoidance in Complex Dynamic Environment
Distance-Based Constraint
$$ \Vert \mathrm{FK}(\vq) - \vx_{\mathrm{obs}}\Vert > \delta $$
Primitive-Based Approximation
e.g., Spheres, Cylinders
- Simple Computation
- Globally Well-Defined
- Poor Scalibility for Complex Geometries
Function approximation
e.g., Neural Network
- Powerful Local Representation
- Handle Complex Shapes
- Poor Extrapolating Ability
ReDSDF: Regularized Deep Signed Distance Field
- Simple Computation
- Powerful Local Representation
- Handle Complex Shapes
- Globally Well-Defined
Poor Scalibility for Complex GeometriesPoor Extrapolating Ability- Articulated Objects
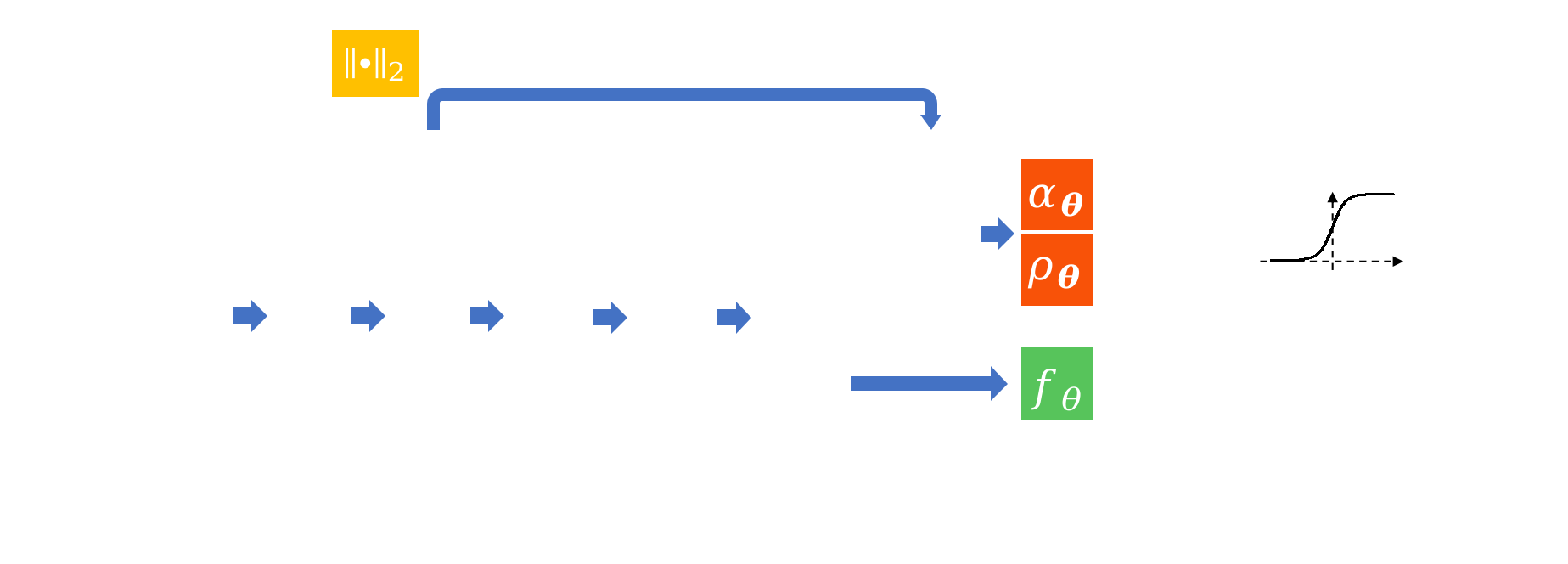
$$ d(\vx, \textcolor{DarkSalmon}{\vq}) = \left[1-\sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\right]\textcolor{LightGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\textcolor{Orange}{\underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
ReDSDF: Regularized Deep Signed Distance Field
$$ d(\vx, \textcolor{DarkSalmon}{\vq}) = \left[1-\sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\right]\textcolor{LightGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\textcolor{Orange}{\underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
$ \sigma_{\vtheta}(\vx, \vq) = \sigmoid\left(\textcolor{OrangeRed}{\alpha_{\vtheta}}\left( \lVert\vx - \vx_c\rVert_2 - \textcolor{OrangeRed}{\rho_{\vtheta}} \right)\right) $
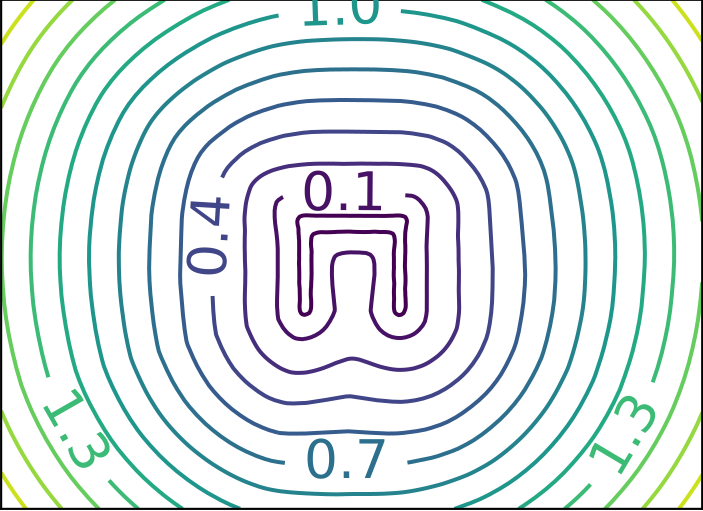
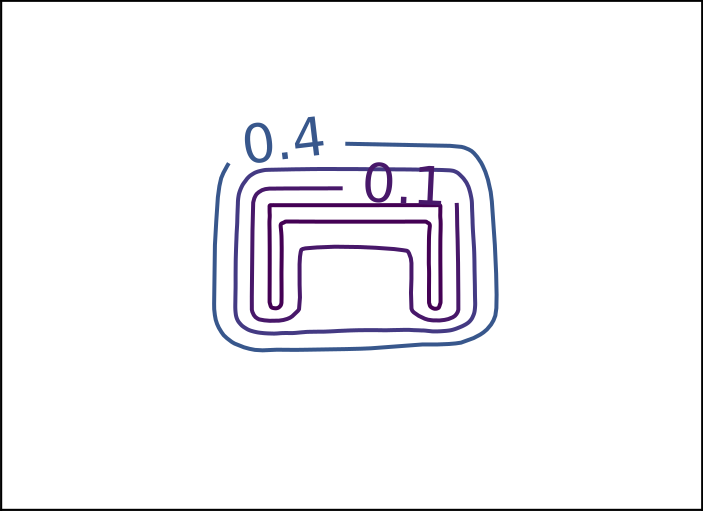
ReDSDF Reconstruction


Table
Shelf




Table
Shelf
Tiago
Human
ReDSDF Extrapolation

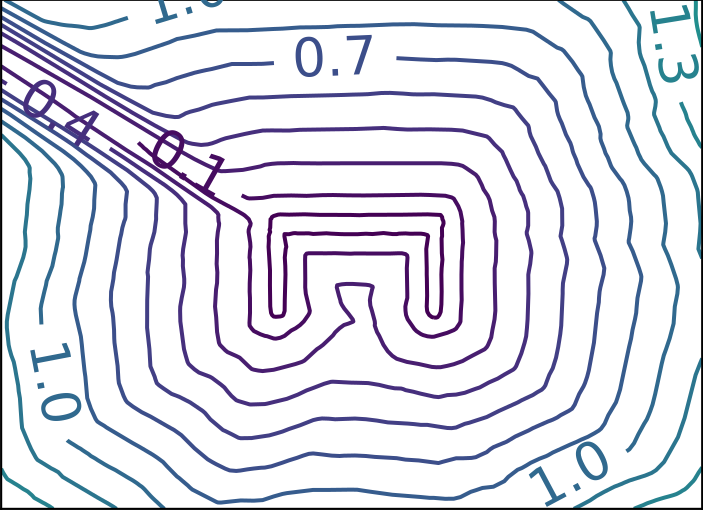

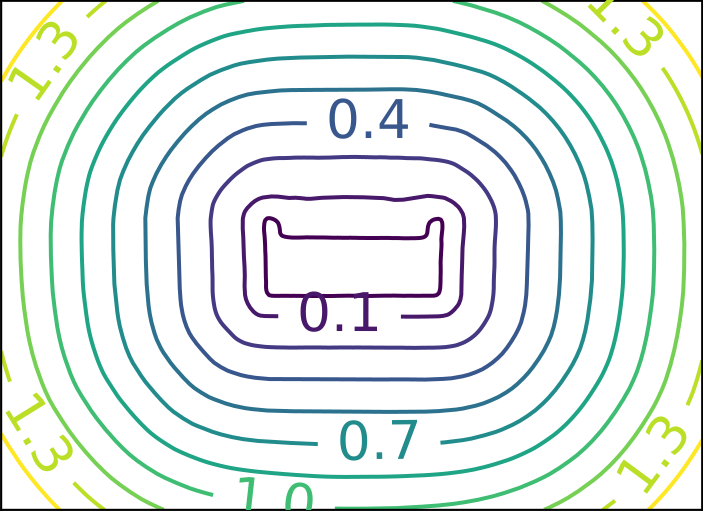
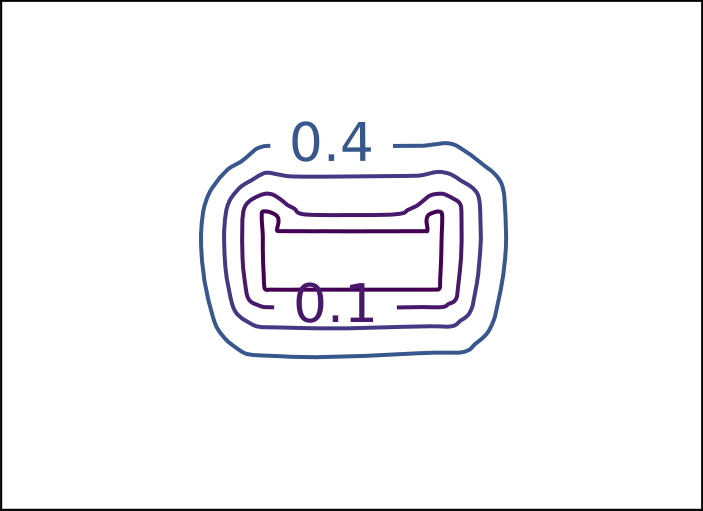
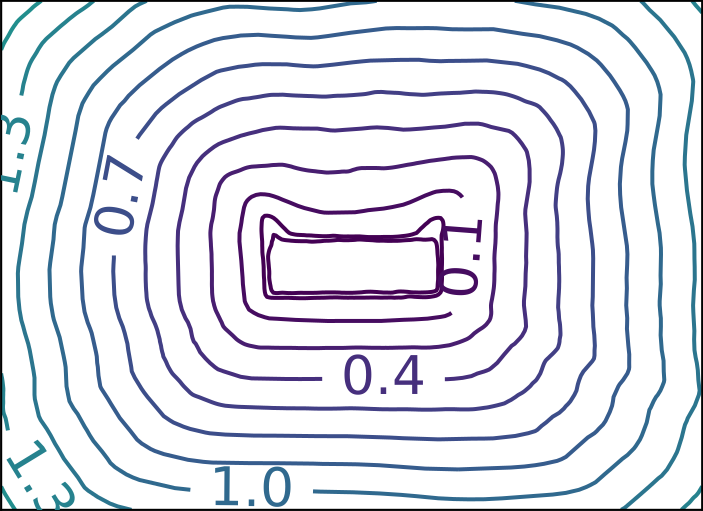


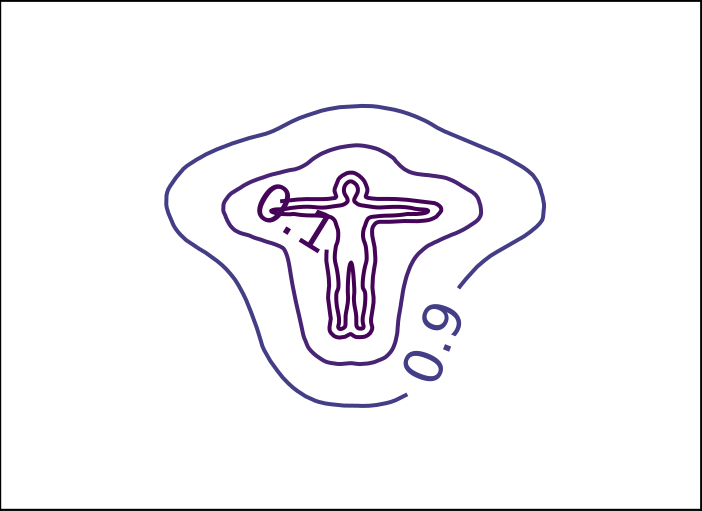
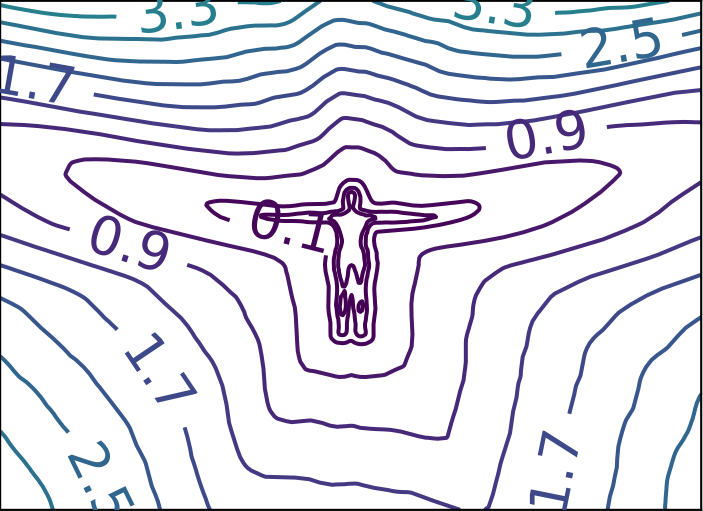
Ground Truth
ReDSDF
DeepSDF
ECMNN
Smooth Varying Distance Field in a Handover Scenario
Reinforcement Learning for Manipulation Task
Manipulation Task
TableEnv
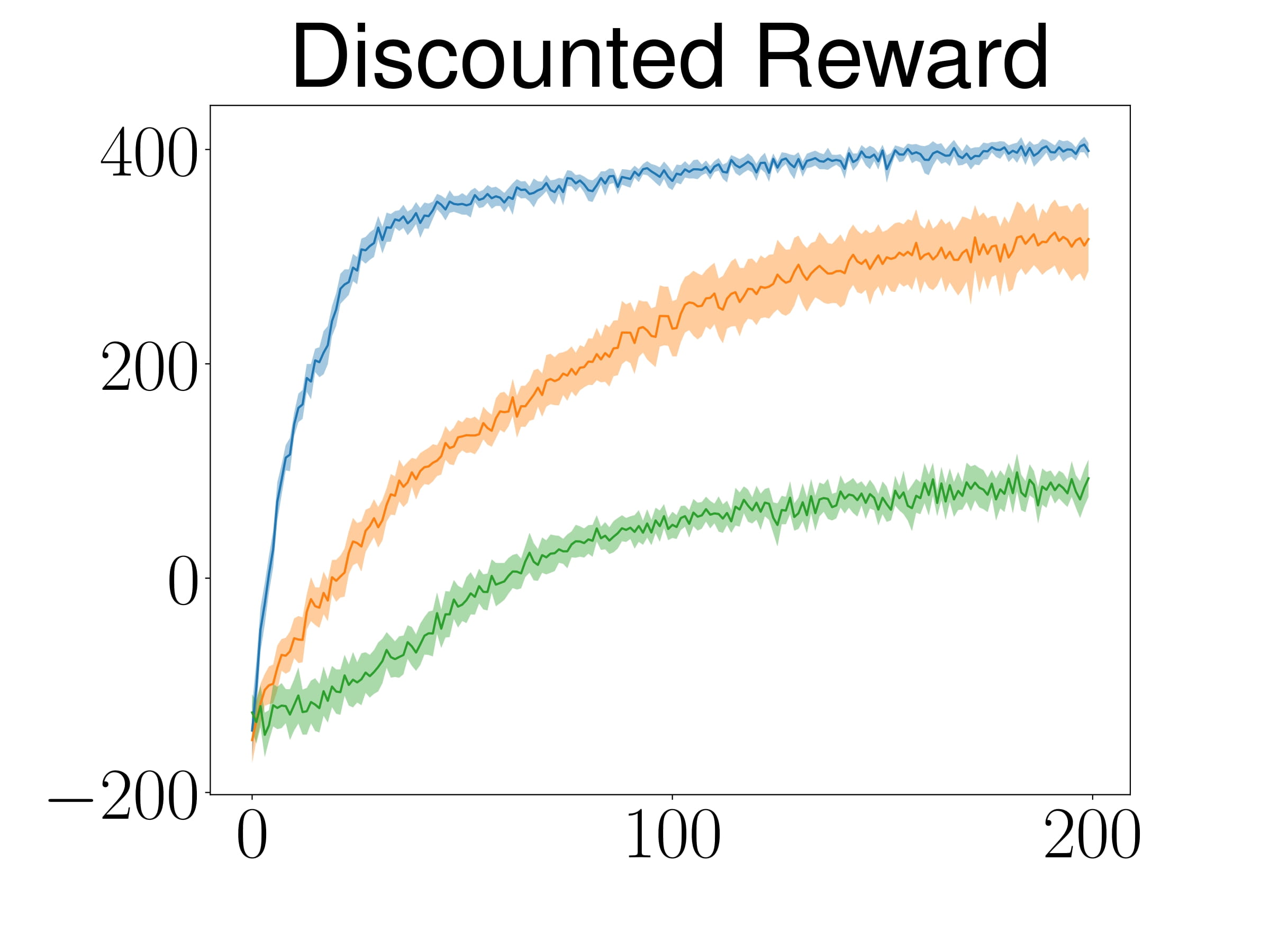
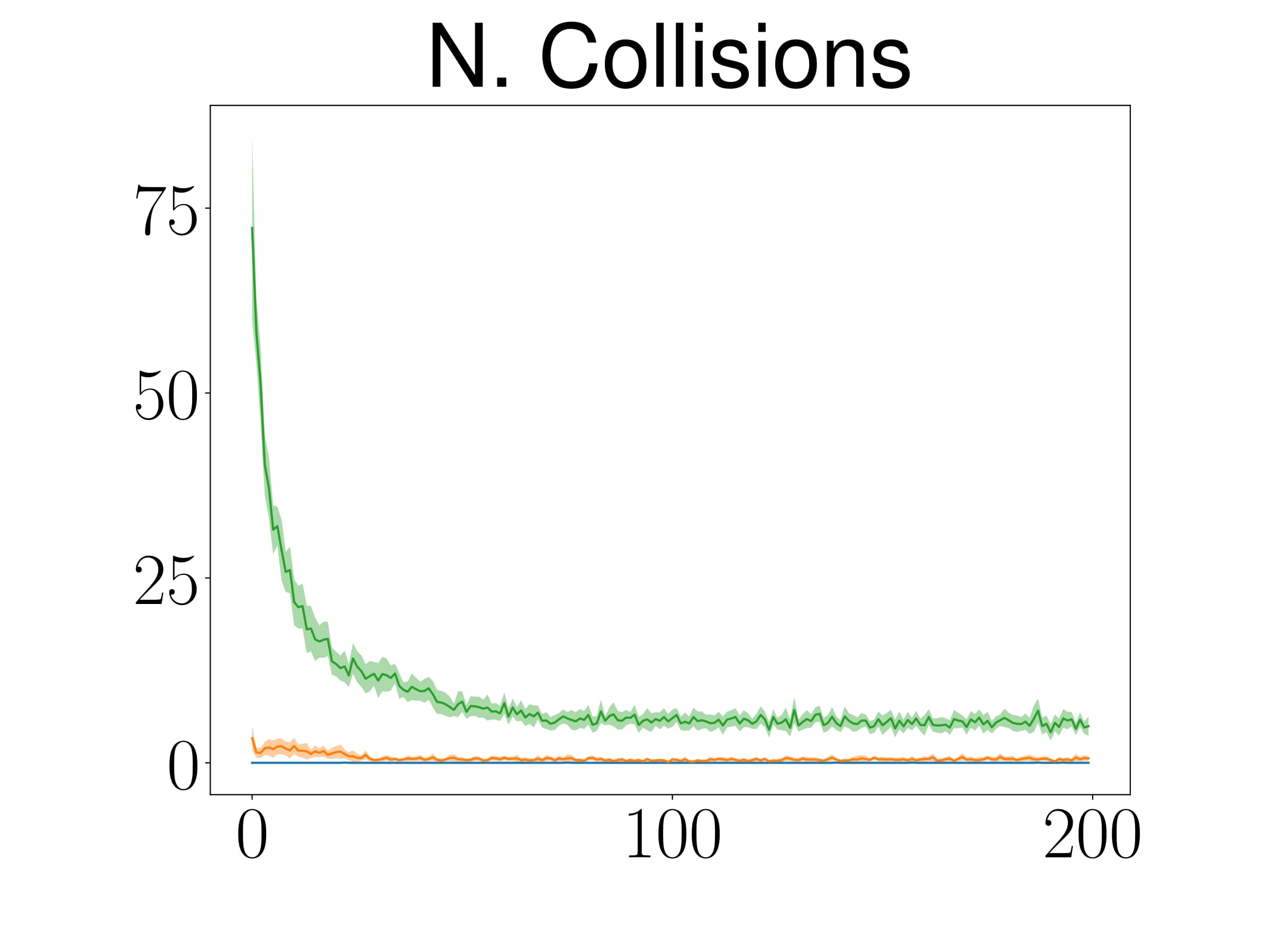
ShelfEnvSim
Human Robot Interaction: Real-Sim
Human Robot Interaction
3x speed
Human Robot Interaction
3x speed
Air Hockey Challenge
Qualifying Stage
air-hockey-challenge.robot-learning.net
Hit
Defend
Prepare
Tournament Stage
air-hockey-challenge.robot-learning.net
Wrap Up

ATACOM: Safe Exploration on the Tangent Space of the Constraimt Manifold

Safe Exploration in Dynamic Environment with Control Affine System

ReDSDF: Regularized Deep Signed Distance Field for Safe Learning and Control>
