Regularized Deep Signed Distance Fields for Reactive Motion Generation
Puze Liu, Kuo Zhang, Davide Tateo, Snehal Jauhri, Jan Peters, and
Georgia Chalvatzaki
Techinal University Darmstadt

Robots in Factory


Robot in Daily Life
- Safety



Robot in Daily Life
- Safety
- Unstructured Environments
- Delicate Manipulation
- Dynamical Human Behavior
How can we achieve dexterous
manipulation task in dynamic
environments without
collisions?



Distance-based Constraints
Primitives approximation
Spheres, Cylinders
- Simple Computation
- Globally Well-Defined
- Poor Scalibility for Complex Geometries
Function approximation
Neural Network
- Powerful Local Representation
- Handle Complex Shapes
- Poor Extrapolating Ability
ReDSDF: Regularized Deep Signed Distance Field
- Simple Computation
- Globally Well-Defined
- Powerful Local Representation
- Handle Complex Shapes
- Poor Scalibility for Complex Geometries
- Poor Extrapolating Ability
- Articulated Objects
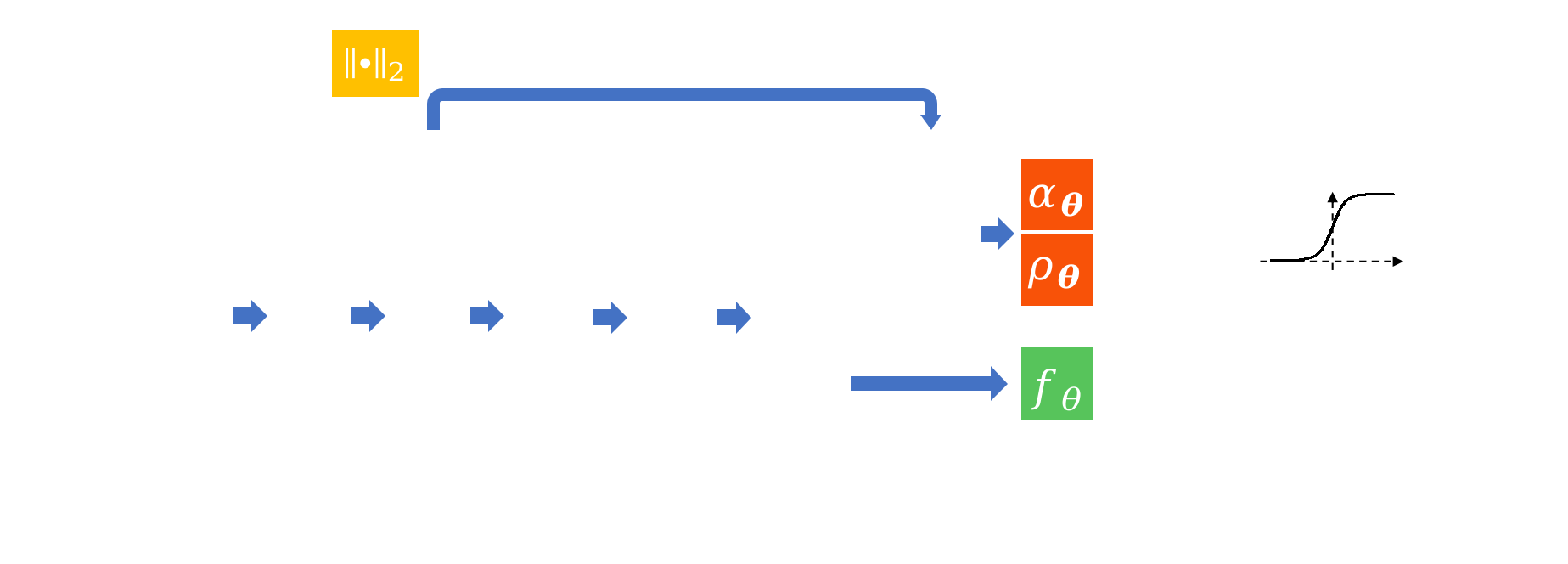
$$ d_{\vq}(\vx) = \left[1-\sigma_{\vtheta}(\vx, \vq)\right]\textcolor{YellowGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \vq)\textcolor{orange}{\underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
ReDSDF: Regularized Deep Signed Distance Field
$$ d_{\vq}(\vx) = \left[1-\sigma_{\vtheta}(\vx, \vq)\right]\textcolor{YellowGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \vq)\textcolor{orange}{\underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
$ \sigma_{\vtheta}(\vx, \vq) = \sigmoid\left(\textcolor{OrangeRed}{\alpha_{\vtheta}}\left( \lVert\vx - \vx_c\rVert_2 - \textcolor{OrangeRed}{\rho_{\vtheta}} \right)\right) $
Data Augmentation and Training
Obtain Point
Cloud
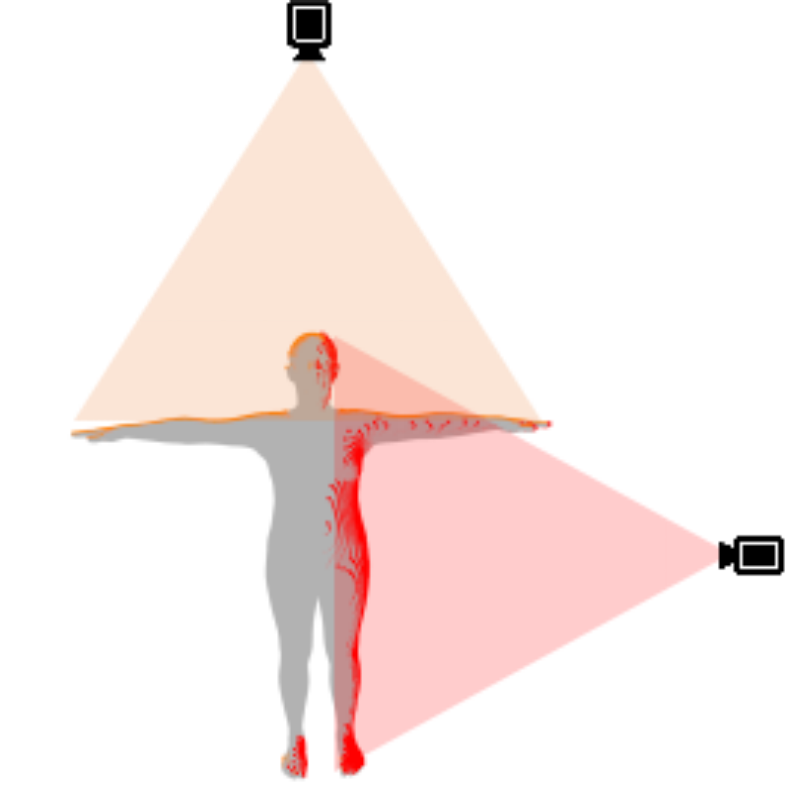
Obtain Point
Cloud


Estimate Normal
Directions
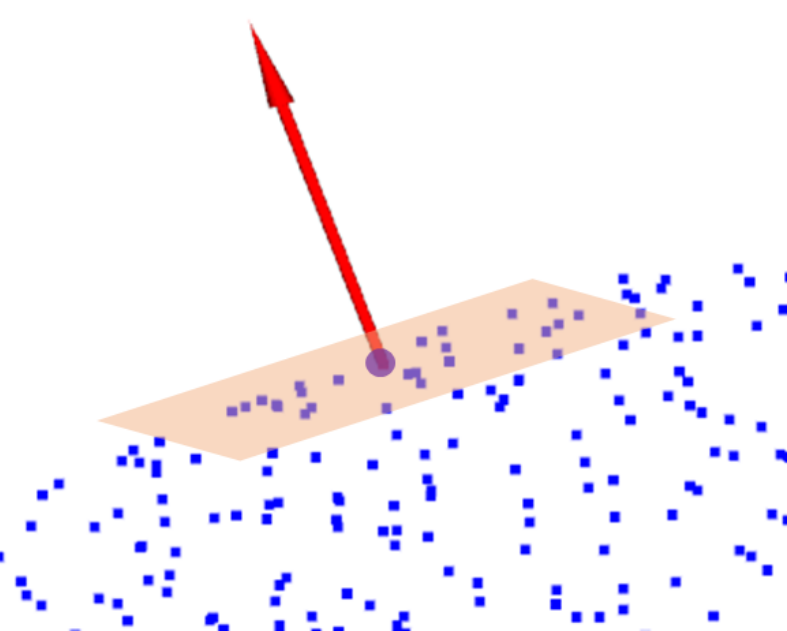

Obtain Point
Cloud


Estimate Normal
Directions


Filter Out
Outliers

Obtain Point
Cloud


Estimate Normal
Directions


Filter Out
Outliers


Augment Data
Point
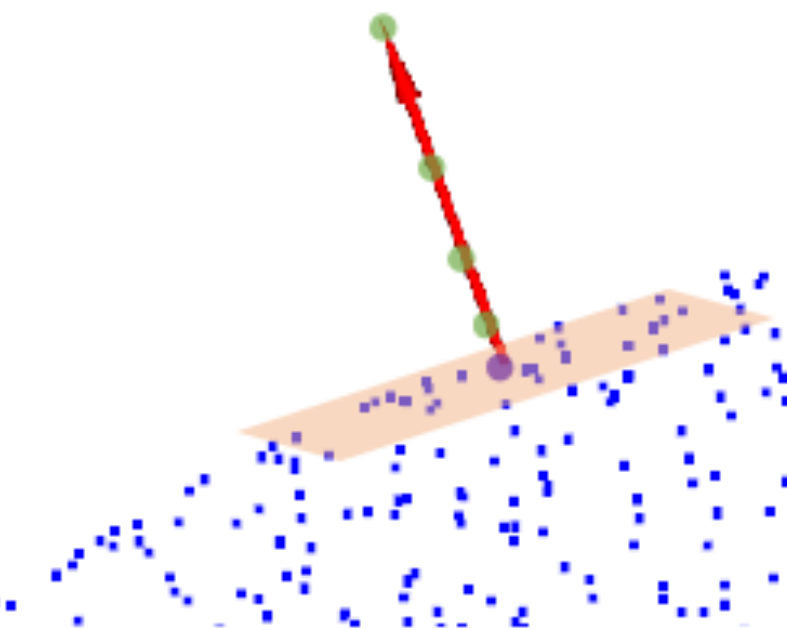
Obtain Point
Cloud


Estimate Normal
Directions


Filter Out
Outliers


Augment Data Point


Down Sampling
$$ \mathcal{L}(\mathcal{D}) = \sum_{\mathcal{D}} \underbrace{\omega_{\vq}(\vx)\left(\bar{d}_{\vq}(\vx) -d_{\vq}(\vx)\right)^2}_{\mathrm{Weighted\,MSE}} + \underbrace{\left( \lVert D_{\vq}(\vx)\bar{\vn}_{\vq}(\vx)\rVert^2_2 + \lVert N_{\vq}(\vx)\nabla_{\vx} d_{\vq}(\vx)\rVert^2_2 \right)}_{\mathrm{Normal\, Direction\; Alignment}} + \underbrace{\gamma\rho_{\vtheta}(\vx,\vq)^2}_{\mathrm{Regularizer\,\\Switching\,Radius}} $$
Obtain Point
Cloud


Estimate Normal
Directions


Filter Out
Outliers


Augment Data Point


Down Sampling


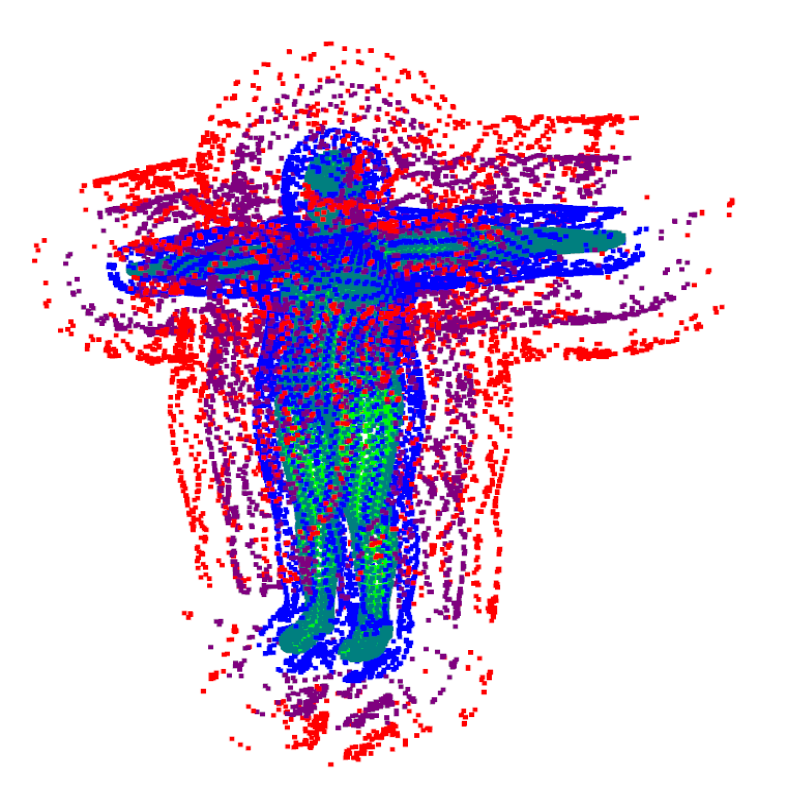
ReDSDF Reconstruction

Table

Shelf
ReDSDF Reconstruction

Table

Shelf

Tiago

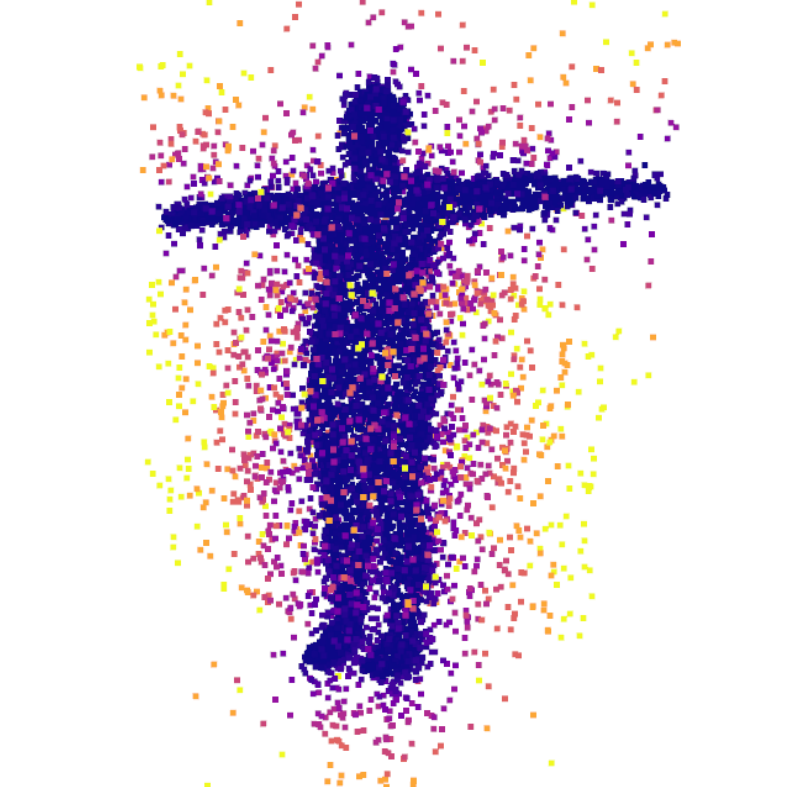
Human
ReDSDF Extrapolation Results

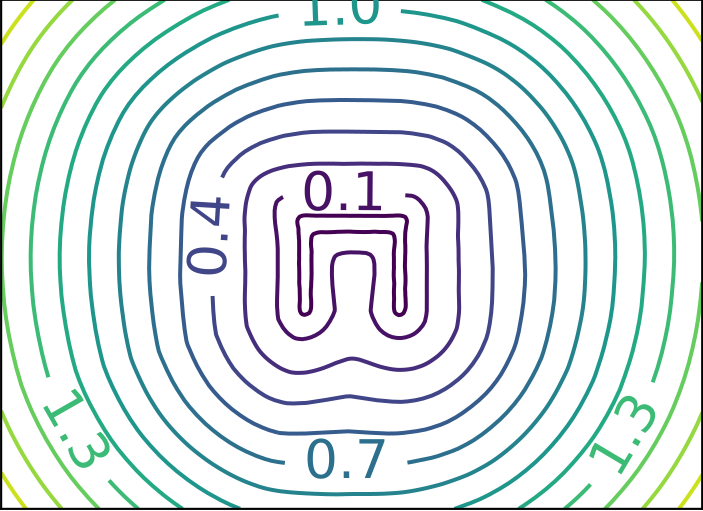
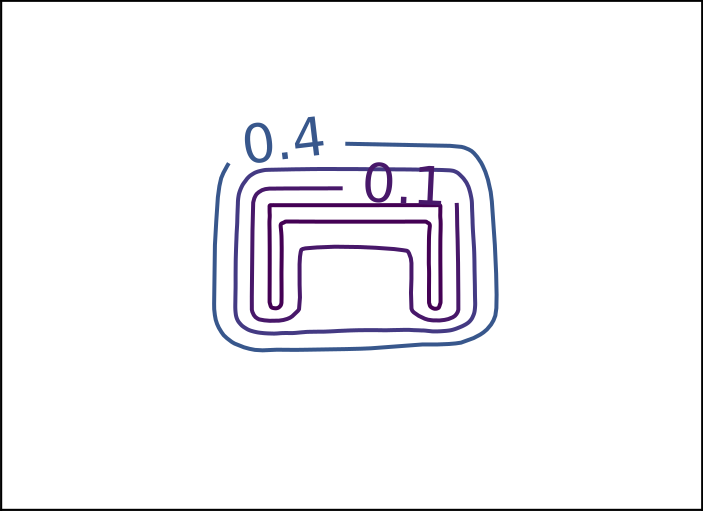
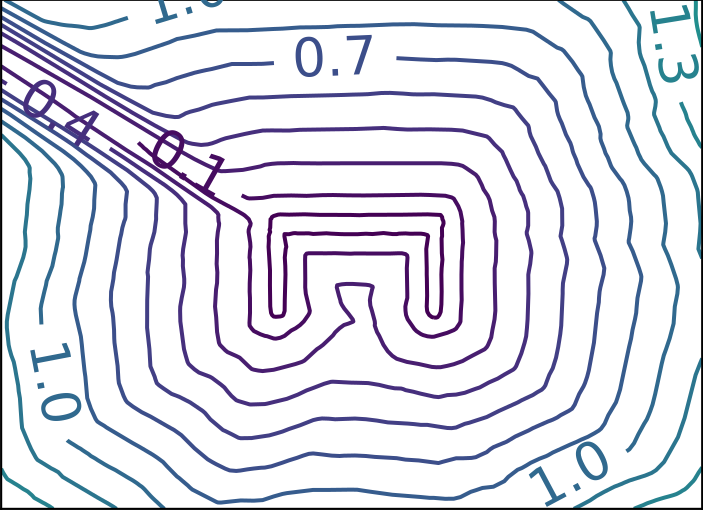

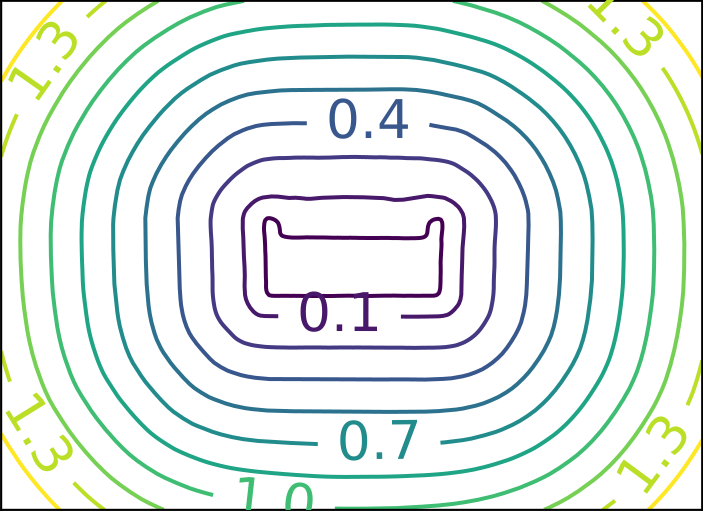
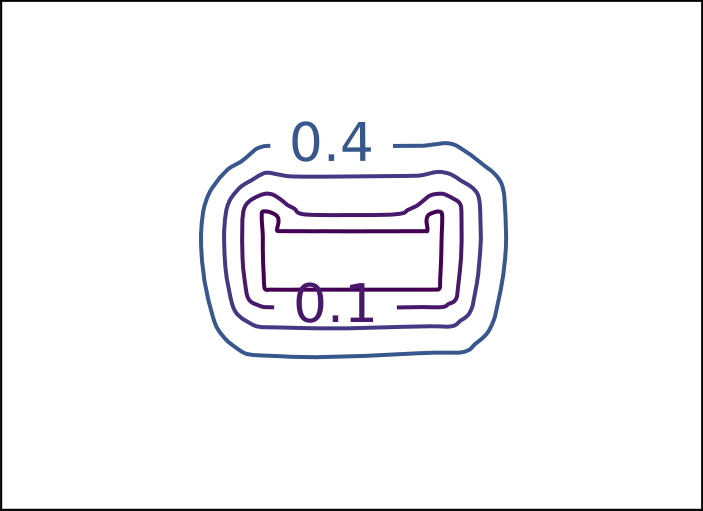
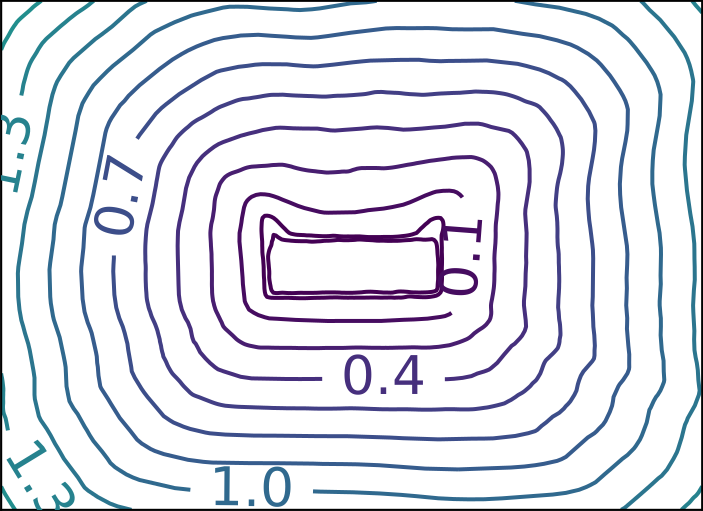


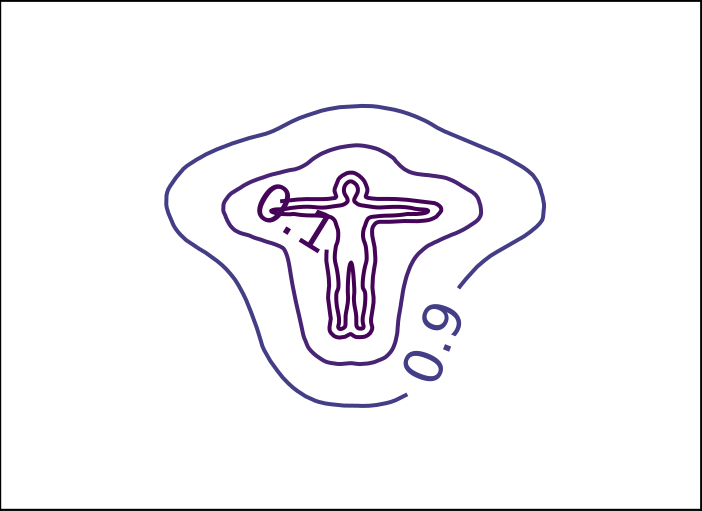
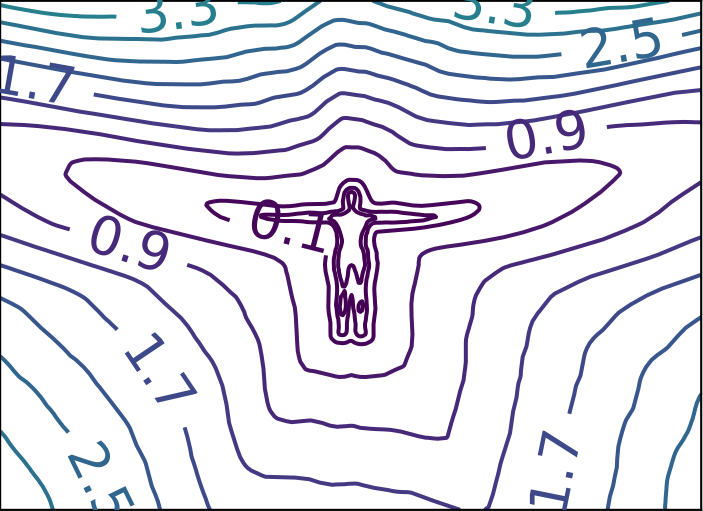
Ground Truth
ReDSDF
DeepSDF
ECMNN
Reactive Motion Generation: Distance Computation

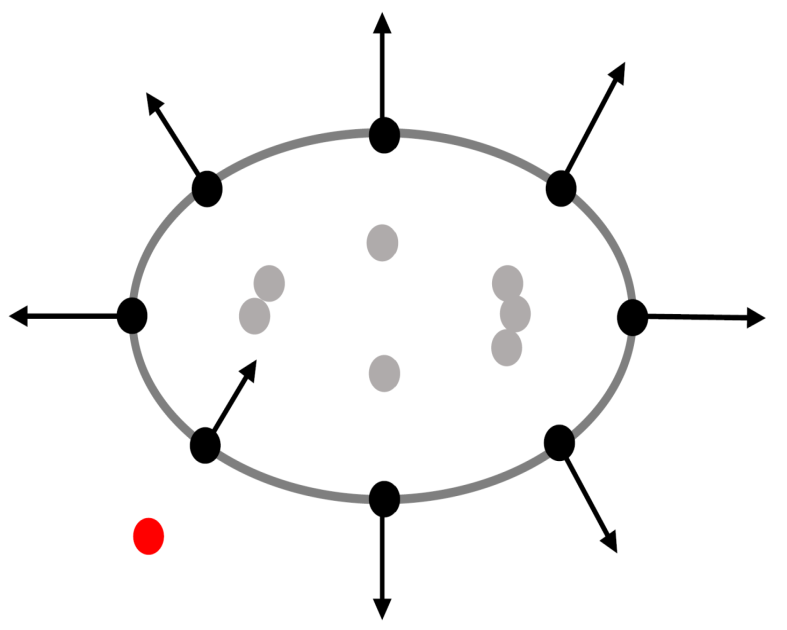
ReDSDF: Points of Interest

Sphere Approximation
Reactive Motion Generation: Bi-Manipulation
No Avoidance
Collision
Sphere Based
Oscillation
ReDSDF
Smooth Motion
Human Robot Interaction
Distance Field:
$\;\frac{1}{3}
\vd_{\mathrm{human,robot}} - 0.25$
Human Robot Interaction
Distance Field:
$\;\frac{1}{3} \vd_{\mathrm{human,robot}} - 0.25$
Distance Field at 0.1m
Take Home Message
Regularized Deep
Signed Distance Fields
Provides A Smooth, Fine-Grained Distance Function
at Any Scale for Articulated Objects
