
Safe Reinforcement Learning of Dynamic High-Dimensional Robotic Tasks: Navigation, Manipulation, Interaction
Puze Liu, Kuo Zhang, Davide Tateo, Snehal Jauhri, Zhiyuan Hu, Jan Peters, and Georgia
Chalvatzaki
Techinal University Darmstadt

Motivation
Dexterous Manipulation, OpenAI
Agile Soccer, DeepMind
How to build safe and reliable reinforcement learning algorithms for robotic system?
Dexterous Manipulation, OpenAI
Agile Soccer, DeepMind
How to build safe and reliable reinforcement learning algorithms for robotic system?
- Typical SafeRL approaches do not ensure safety during training.
- Online training is often necessary to briged the sim-to-real gap.
- Safe Exploration methods often require extra engineering.
- Ensuring safety in dynamic environment with high-dimensional system is challenging.
Problem Formulation
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & c(\vs_t) < 0 \end{align*}$$ with $\vs_t \in \RR^{S}$ and $c:\RR^{S}\rightarrow \RR^{N}$
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & c(\vs_t) < 0 \end{align*}$$ with $\vs_t \in \RR^{S}$ and $c:\RR^{S}\rightarrow \RR^{N}$
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & c(\vs_t) + h(\vmu_t) = 0 \end{align*}$$ with $\vmu_t \in \RR^{N}$ and $h:\RR^{N}\rightarrow \RR^{N}_{+}$
ATACOM
Construct a Constraint Manifold and a corresponding Action Space that enables control actions to move state along the Tangent Space of the constraint manifold.
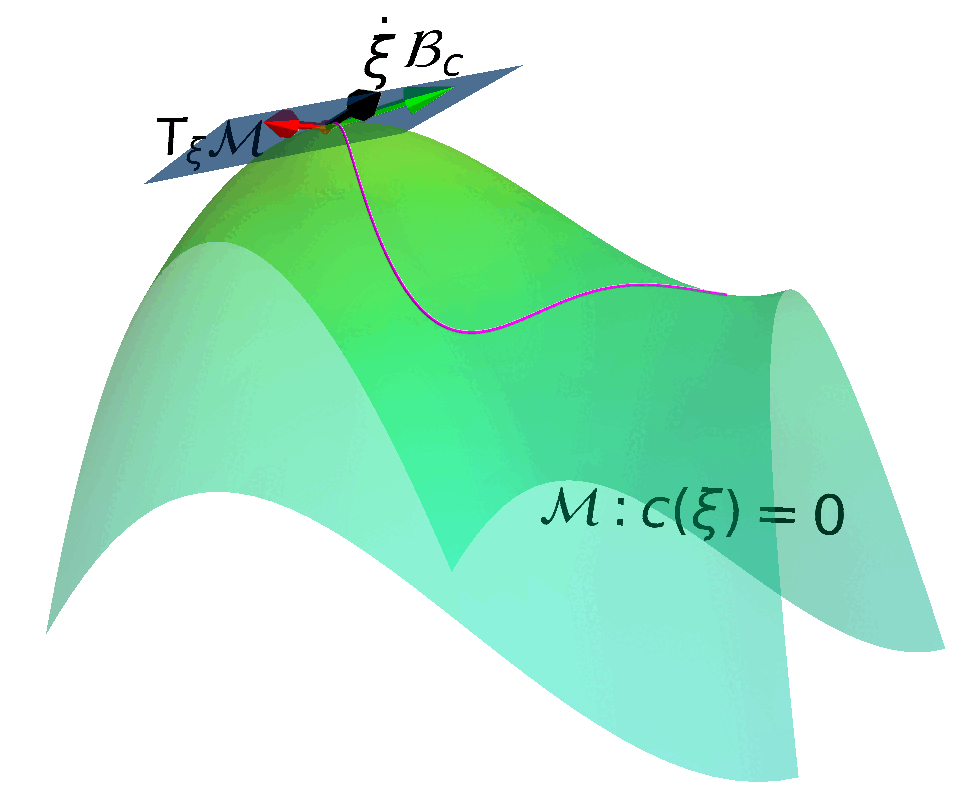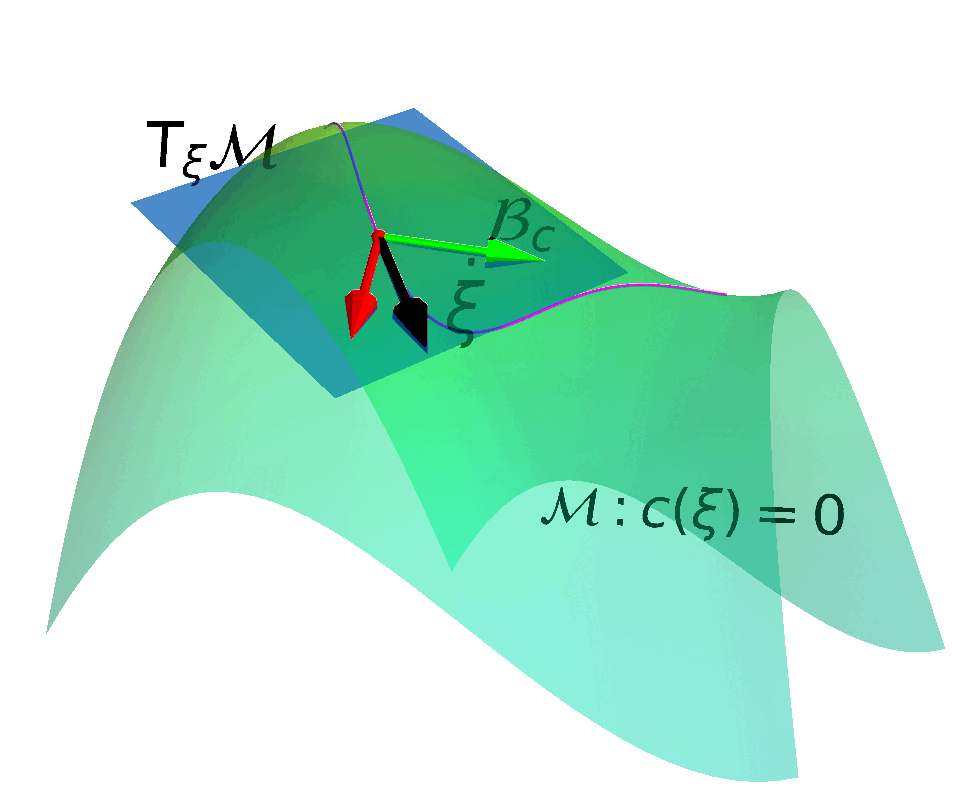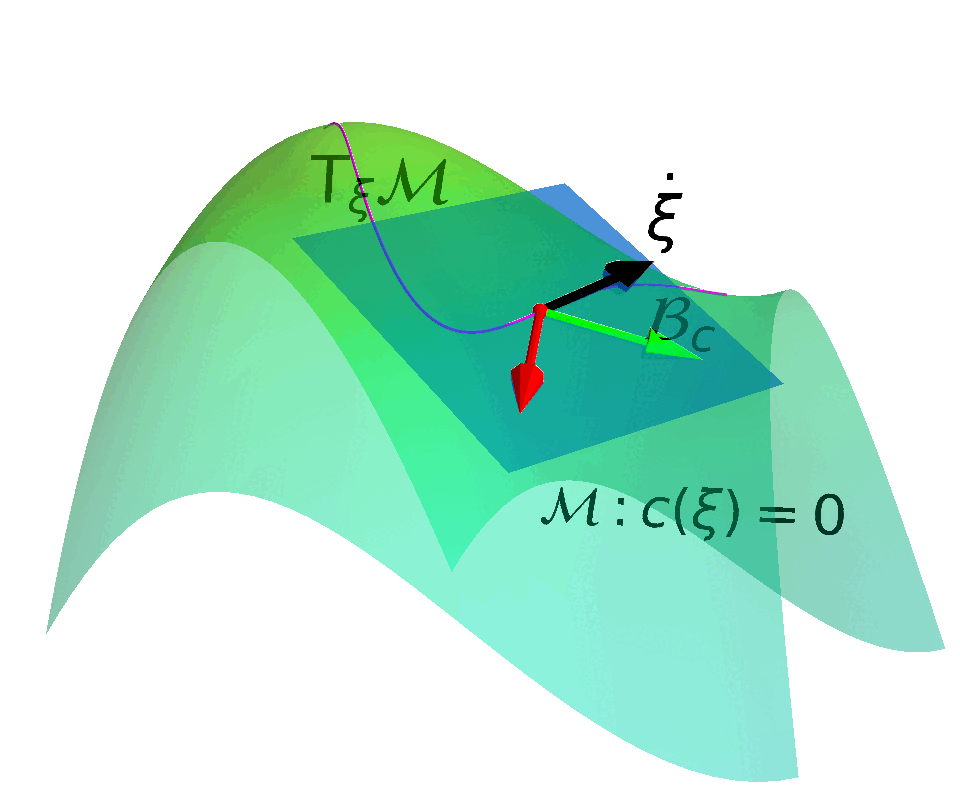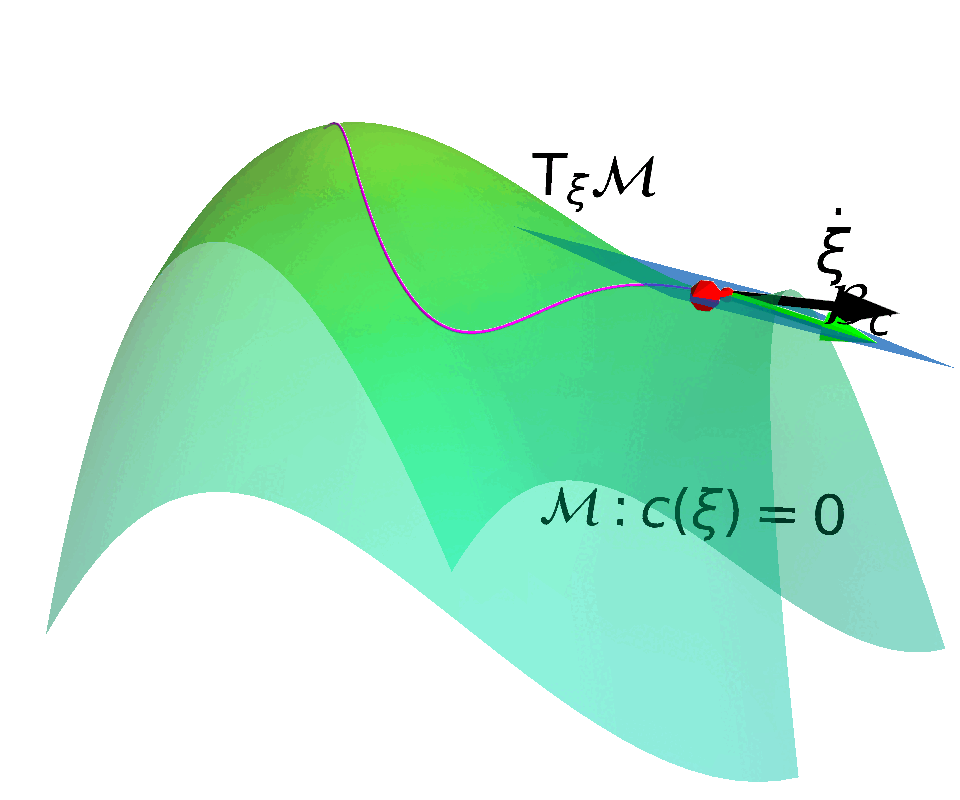
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & c(\vs_t) + h(\vmu_t) = 0 \end{align*}$$ with $\vmu_t \in \RR^{N}$ and $h:\RR^{N}\rightarrow \RR^{N}_{+}$
Limitations
ATACOM
Construct a Constrained Manifold and a corresponding Action Space that enables control actions to move state along the Tangent Space of the constrained manifold.

ATACOM Controller
Acting on the TAgent Space of the COnstraint Manifold
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & c(\vs_t) + h(\vmu_t) = 0 \end{align*}$$ with $\vmu_t \in \RR^{N}$ and $h:\RR^{N}\rightarrow \RR^{N}_{+}$
Limitations
Improvements
1. Separable State Space
$$ \vs = \begin{bmatrix}\vq \\ \vx \end{bmatrix} $$ with $\vq_t \in \RR^{Q}$ and $\vx_t \in \RR^{X}$, $S = Q + X$
2. Control Affine System
$$ \dot{\vq} = f(\vq) + G(\vq) \va $$
3. SoftCorner Function
$$h(\mu) = -\frac{1}{\beta}\ln(1 - e^{\beta \mu})$$
Improvements
1. Separable State Space
$$ \vs = \begin{bmatrix}\vq \\ \vx \end{bmatrix} $$ with $\vq_t \in \RR^{Q}$ and $\vx_t \in \RR^{X}$, $S = Q + X$
2. Control Affine System
$$ \dot{\vq} = f(\vq) + G(\vq) \va $$
3. SoftCorner Function
$$h(\mu) = -\frac{1}{\beta}\ln(1 - e^{\beta \mu})$$
Constraint Manifold
$$ \MM = \{ (\vq, \vx, \vmu)\in \RR^{Q+X+N}: \bar{c}(\vq, \vx, \vmu) = \vzero \} $$
with $\bar{c}(\vq, \vx, \vmu) := c(\vq, \vx) + h(\vmu)$.
Improved ATACOM Controller
$$ \begin{bmatrix} \va \\ \dot{\vmu} \end{bmatrix} = \underbrace{-\mJ_{[G, \mu]}^{\dagger} \mF(\vq, \vx, \dot{\vx}, \vmu)}_{\text{Drift Compensation Term}} \underbrace{- K_c \mJ_{[G, \mu]}^{\dagger} \bar{c}(\vq, \vx, \vmu)}_{\text{Contraction Term}} \underbrace{+\mN_{[G, \mu]} \valpha}_{\text{Tangent Term}}$$
Comparison of Slack Variable Function
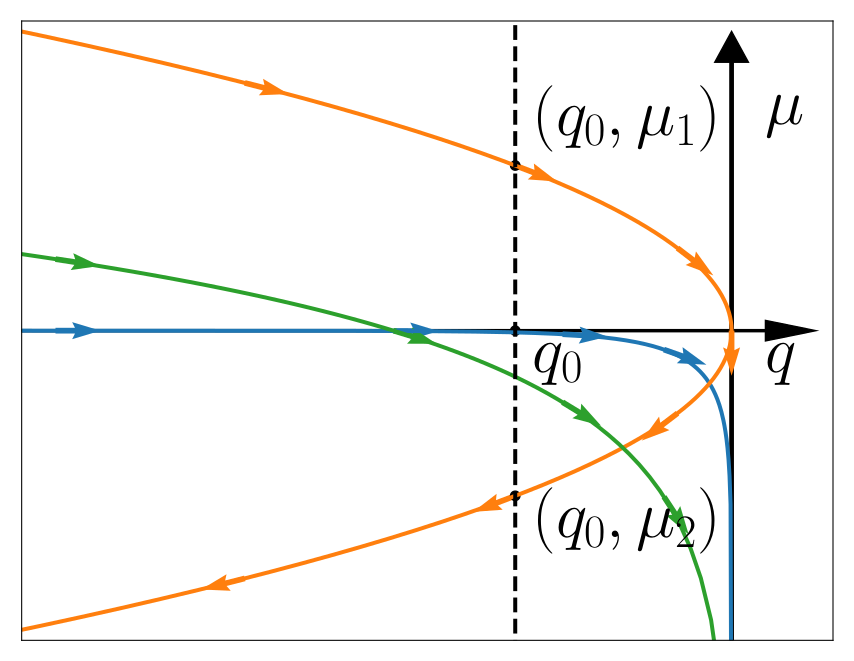
Constraint Manifold: $ q + h(\mu) = 0$
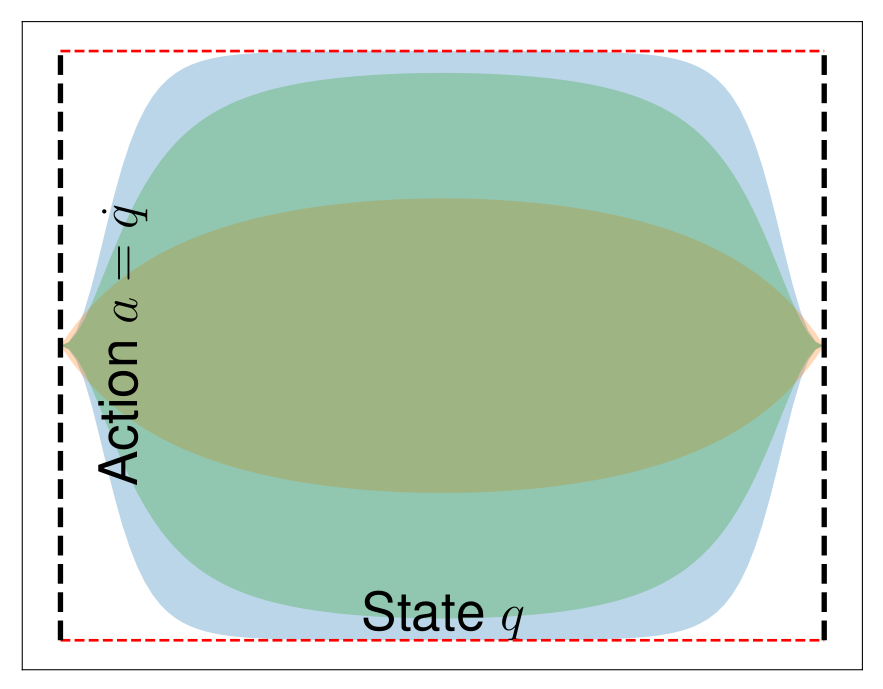
Action Space for $ -1 < q < 0 $
$h(\mu)$:
Collision Avoidance in Robotics

Dynamical Environment
- Stand-alone robot that moves blindly to the goal.
- Differential drive as a control affine system.
$$ \vq = \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} \quad f(\vq) = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \quad G(\vq) = \begin{bmatrix} \cos(\theta) & 0 \\ \sin(\theta) & 0 \\ 0 & 1 \end{bmatrix} \quad \va = \begin{bmatrix} v \\ \omega \end{bmatrix}$$
SAC
- Stand-alone robot that moves blindly to the goal
- Differential drive as a control affine system
$$ \vq = \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} \quad f(\vq) = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \quad G(\vq) = \begin{bmatrix} \cos(\theta) & 0 \\ \sin(\theta) & 0 \\ 0 & 1 \end{bmatrix} \quad \va = \begin{bmatrix} v \\ \omega \end{bmatrix}$$
SAC
SafetyLayer
ATACOM - SAC
Collision Avoidance in Robotics

Dynamical Environment

Dynamical Environment

Complex Geometries

Dynamical Environment

Complex Geometries

Deformable Objects
ReDSDF: Regularized Deep Signed Distance Field




Table
Shelf
Tiago
Human
Manipulation Task
Human Robot Interaction: Real-Sim
Human Robot Interaction
3x speed
Human Robot Interaction
3x speed
Wrap Up
Improved ATACOM enables safe exploration with control affine system in dynamical environment.
