Safe Reinforcement Learning on the Constraint Manifold
Puze Liu
German Research Center for AI

Reinforcement Learning in Robotics
Robot Parkour (2023), Qi Zhi Lab, Stanford
Robot Parkour (2023), Qi Zhi Lab, Stanford
Robot Soccer (2023), Deepmind
Robot Parkour (2023), Qi Zhi Lab, Stanford
Robot Soccer (2023), Deepmind
Humanoid Backflip (2024), Unitree
Robot Parkour (2023), Qi Zhi Lab, Stanford
Robot Soccer (2023), Deepmind
Humanoid Backflip (2024), Unitree
- Policy trained in simulation
- Domain randomization to increase the robustness
- Zero shot transfer without real-world fine tuning
- Simulator that captures environment variations
- Failure in unforeseen scenarios
- Robot lacks of performance improving capability
Robot Parkour (2023), Qi Zhi Lab, Stanford
Robot Soccer (2023), Deepmind
Humanoid Backflip (2024), Unitree
Keep robots learning while interacting with the real world
Keep Robots Learning while Safely Interacting with the Real World!

Safe Exploration
Design safe policies under given constraints

Safety Constraint
Learn safety constraints for complex environments
Safe Exploration
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & k(\vs_t) < 0 \end{align*}$$
Robot dynamics $\dot{\vs} = f(\vs) + G(\vs) \vu_s $
$$ \begin{align*} \max_{\pi} \quad & \mathbb{E}_{\tau \in \pi} \left[ \sum_{t}^{T} \gamma^t r(\vs_t, \va_t) \right] \\ \mathrm{s.t.} \quad & k(\vs_t) < 0 \end{align*}$$
Robot dynamics $\dot{\vs} = f(\vs) + G(\vs) \vu_s $
Core Idea
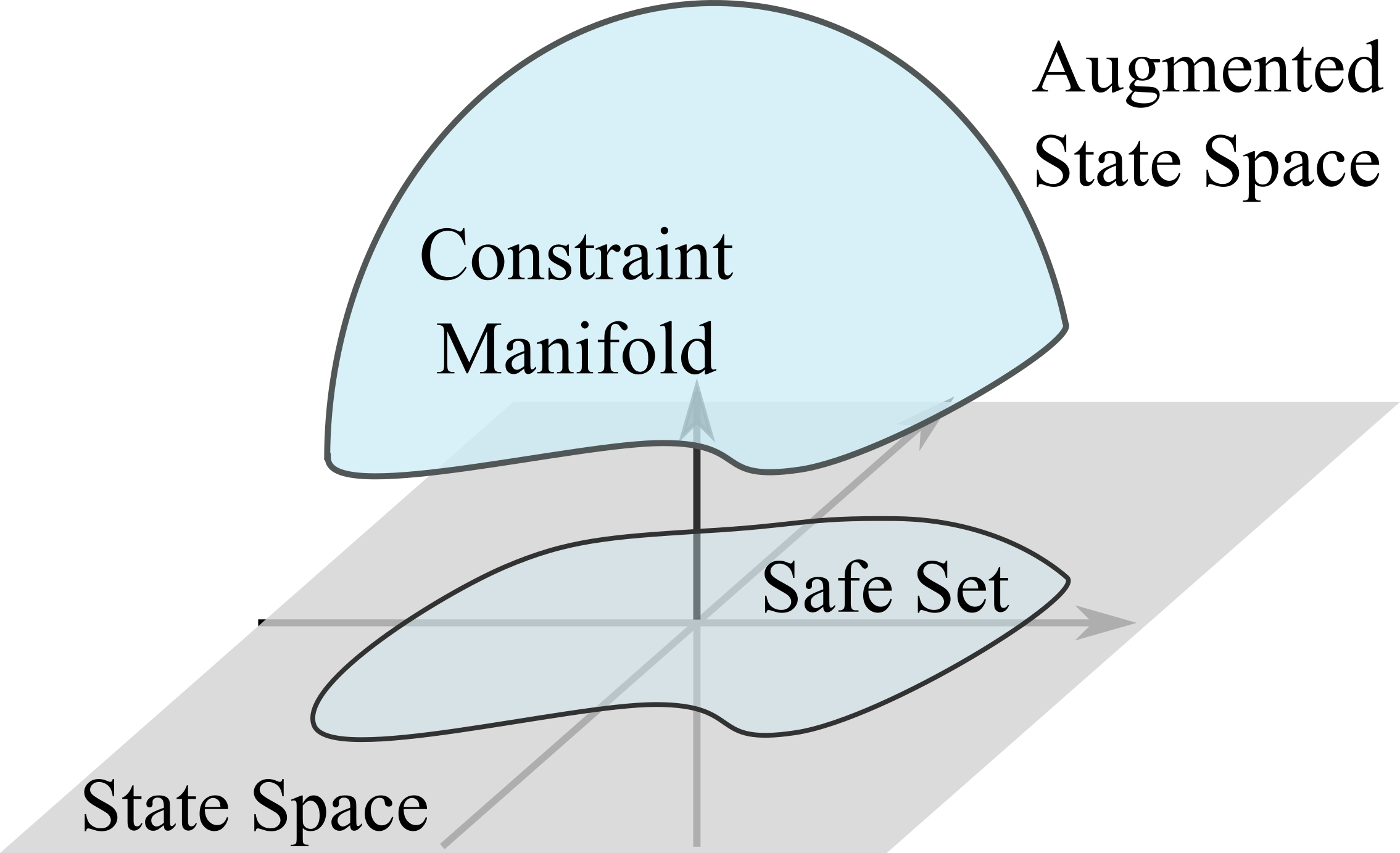
Convert the constraint into a constraint manifold and construct a safe action space that drives the state tangent to the constraint manifold.

Constraint Manifold
Safe Set $\quad \mathcal{C} = \{\vs \in \mathcal{S} | k(\vs) < 0 \}$
Constraint Manifold in Augmented State Space $$ \MM = \{(\vs, \vmu) \in \mathcal{S} \times \mathbb{R}^{+} | c(\vs, \vmu) \coloneqq k(\vs) + \vmu = 0\} $$
Dynamics for Slack Variable $$\dot{\vmu} = A(\vmu) \vu_{\mu}$$ $A$ is continuous, strictly increasing and $A(\vzero) = \vzero$
Augmented Dynamics $$\begin{bmatrix}\dot{\vs} \\ \dot{\vmu} \end{bmatrix} =\begin{bmatrix} f(\vs) \\ \vzero \end{bmatrix} + \begin{bmatrix} G(\vs) & \vzero \\ \vzero & A(\vmu) \end{bmatrix} \begin{bmatrix} \vu_s \\ \vu_{\mu} \end{bmatrix}$$
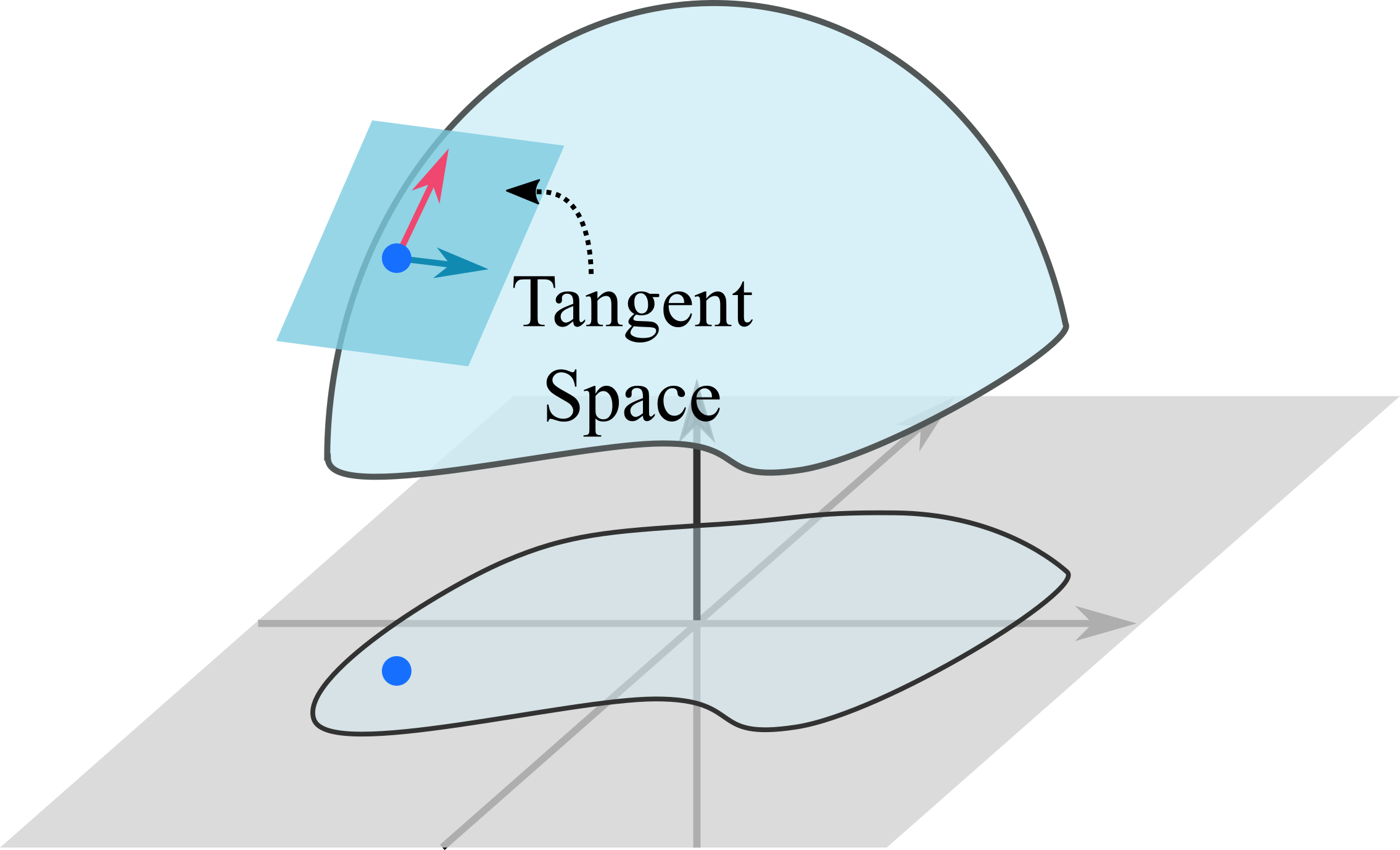
Tangent Space of the Constraint Manifold
Velocity tangent to the manifold $$\mathrm{T}_{(s, \mu)}\MM =\left\{ (\dot{\vs}, \dot{\vmu}) | \dot{c}(\vs, \vmu) = \begin{bmatrix} \mJ_k & \mathbb{I} \end{bmatrix} \begin{bmatrix} \dot{\vs} \\ \dot{\vmu} \end{bmatrix} = \vzero \right\}$$
Combine with augmented state dynamics $$ \underbrace{\mJ_k\vf}_{\vpsi} + \underbrace{\begin{bmatrix} \mJ_k \mG & \mA \end{bmatrix}}_{\mJ_u} \begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix}= \vzero $$
Acting on the TAngent space of the COnstraint Manifold (ATACOM)
$\begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix} = \textcolor{b2e061}{\underbrace{-\mJ_u^{\dagger} \vpsi}_{\text{Drift Comp.}}}$ $\textcolor{#fd7f6f}{\underbrace{- \lambda \mJ_u^{\dagger} \vc}_{\text{ Contraction }}}$ $\textcolor{7eb0d5}{\underbrace{+ \mB_u \va }_{\text{ Tangential }}} $
ATACOM
Acting on the TAngent space of the COnstraint Manifold (ATACOM)
$\begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix} = \textcolor{b2e061}{\underbrace{-\mJ_u^{\dagger} \vpsi}_{\text{Drift Comp.}}}$ $\textcolor{#fd7f6f}{\underbrace{- \lambda \mJ_u^{\dagger} \vc}_{\text{ Contraction }}}$ $\textcolor{7eb0d5}{\underbrace{+ \mB_u \va }_{\text{ Tangential }}} $
- Nullspace matrix $\mB_u$ such that $\mJ_u \mB_u = \vzero$. $\mB_u$ determines the tangent space basis.
- Drift compensation term and contraction term are determined by $\vs$.
- ATACOM constructs a safe action space $\va \in \mathcal{A}$ and a mapping $W(\va): \mathcal{A} \rightarrow \mathcal{U}$.
- Can be used in various RL methods as all actions are sampled in the safe action space.
Acting on the TAngent space of the COnstraint Manifold (ATACOM)
$\begin{bmatrix} \vu_s \\ \vu_\mu \end{bmatrix} = \textcolor{b2e061}{\underbrace{-\mJ_u^{\dagger} \vpsi}_{\text{Drift Comp.}}}$ $\textcolor{#fd7f6f}{\underbrace{- \lambda \mJ_u^{\dagger} \vc}_{\text{ Contraction }}}$ $\textcolor{7eb0d5}{\underbrace{+ \mB_u \va }_{\text{ Tangential }}} $
Velocity Controlled System: $\dot{s} = u_s$
Constraint: $s^2 < 1$
Constraint Manifold: $$\MM = \{(s, \mu) | s^2 + \mu -1 = 0 \} $$
$$\psi = 0, a=1$$
$$J_u = \begin{bmatrix} 2s & \mu \end{bmatrix}, B_u=\begin{bmatrix} -\mu \\ 2s \end{bmatrix}$$

Robot Air Hockey Experiment
- Task: hit the randomly initialized puck to the goal
- Control: robot's joint velocity
- Observation: puck and robot's Joint position/velocity
- Constraint:
- Mallet stays on the table surface and within the boundary
- Robot do not collide with the table
- Joint position within the limits
- RL algorithm: ATACOM-SAC
Training result in simulation
- Real world experiment setup
- Motion tracking system to observe puck's position/velocity
- Resetter: Mitsubishi PA10 with a vacuume gripper
- Pre-programmed planning
- Fine-tuning with real world interactions
- Data collection: 100 episodes (~48min)
- Total training: 3000 episodes (~24h)
Real World Experiment Setup
Success rate
| Simulation | 86% |
| Zero-shot transfer | 12% |
| Fine tuning | 71% |
Hitting Velocity
| Simulation | 0.92m/s |
| Zero-shot transfer | 0.97m/s |
| Fine tuning | 0.97m/s |
Limitations and Extensions
1. Separable State Space
$$ \vs = \begin{bmatrix}\vq \\ \vx \end{bmatrix}, \quad \dot{\vq} = f(\vq) + G(\vq) \vu $$
Constraint: $k(\vq, \vx) \leq \vzero$
Drift and Jacobian: $$\vpsi = \mJ_q f + \mJ_x \dot{\vx}$$ $$\mJ_u = \begin{bmatrix} \mJ_q G & A \end{bmatrix}$$
Mobile Robot with Differential Drive
15 Moving Obstacles
Keep Robots Learning during Safe Interactions in the Real World!

Safe Exploration
Design safe policies under given constraints

Safety Constraint
Learn safety constraints for complex environments
Constraints for the Collision Avoidance
Distance-Based Constraint
$$ \Vert \vx_{\mathrm{robot}} - \vx_{\mathrm{obs}}\Vert > \delta $$
Primitives
e.g., Spheres, Cylinders
- Simple Computation
- Globally Well-Defined
- Poor Scalibility for Complex Geometries
Function Approximator
e.g., Neural Network
- Powerful Local Representation
- Handle Complex Shapes
- Poor Extrapolating Ability
ReDSDF: Regularized Deep Signed Distance Field
- Simple Computation
- Powerful Local Representation
- Handle Complex Shapes
- Globally Well-Defined
Poor Scalibility for Complex GeometriesPoor Extrapolating Ability- Articulated Objects
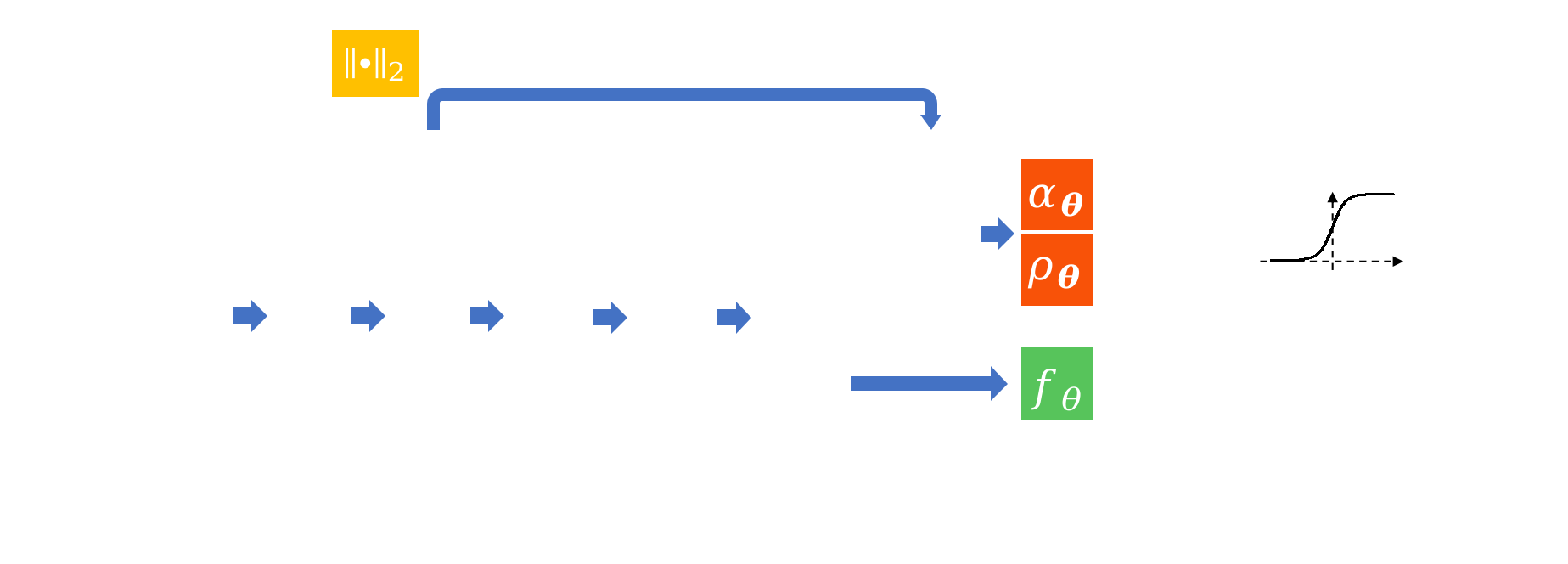
$$ d(\vx, \textcolor{DarkSalmon}{\vq}) = \left[1-\sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\right]\textcolor{LightGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\textcolor{Orange}{\underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
ReDSDF: Regularized Deep Signed Distance Field
$$ d(\vx, \textcolor{DarkSalmon}{\vq}) = \left[1-\sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\right]\textcolor{LightGreen}{\underbrace{f_{\vtheta}(\vx, \vq)}_{\mathrm{NN}}} + \sigma_{\vtheta}(\vx, \textcolor{DarkSalmon}{\vq})\textcolor{Orange}{\underbrace{\lVert \vx - \vx_c \rVert_2}_{\mathrm{Point\,Dist.}}}$$
$ \sigma_{\vtheta}(\vx, \vq) = \sigmoid\left(\textcolor{OrangeRed}{\alpha_{\vtheta}}\left( \lVert\vx - \vx_c\rVert_2 - \textcolor{OrangeRed}{\rho_{\vtheta}} \right)\right) $
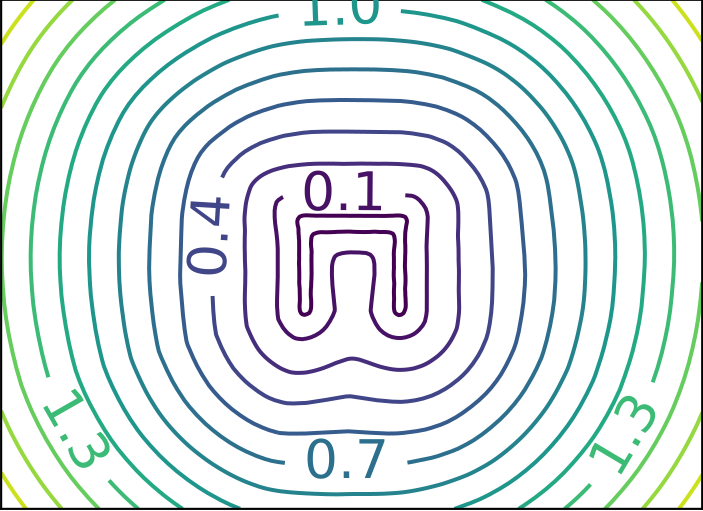
ReDSDF Reconstruction


Table
Shelf




Table
Shelf
Tiago
Human
ReDSDF Extrapolation

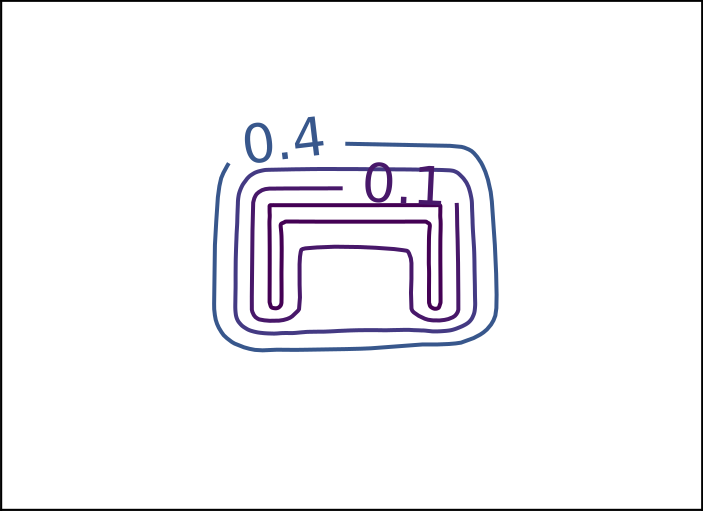
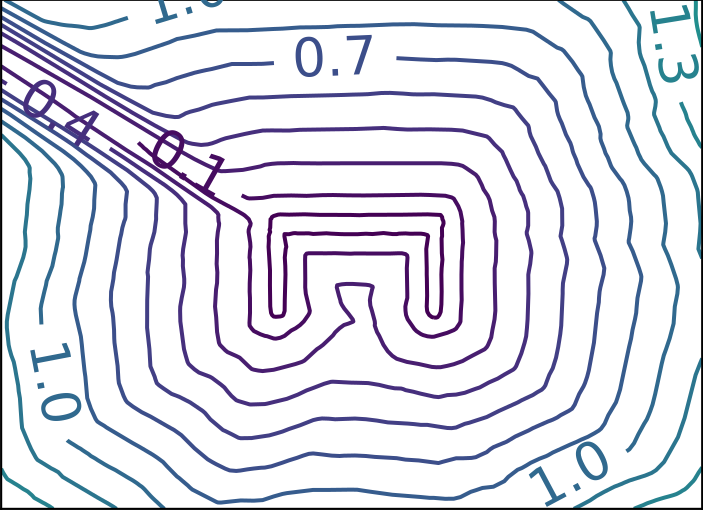

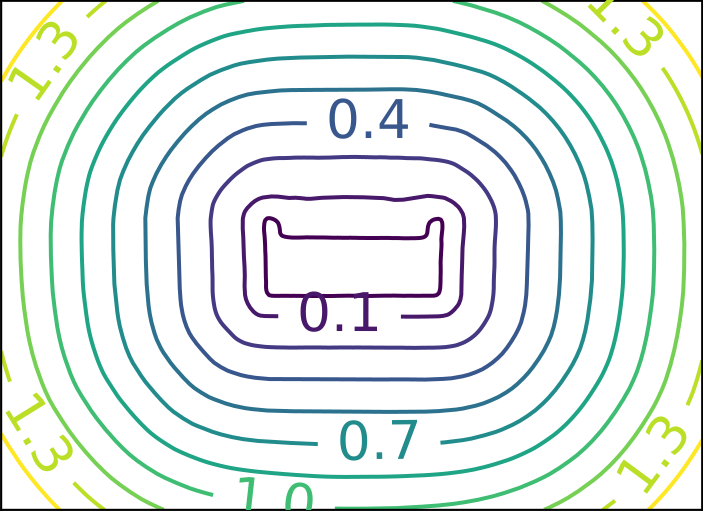
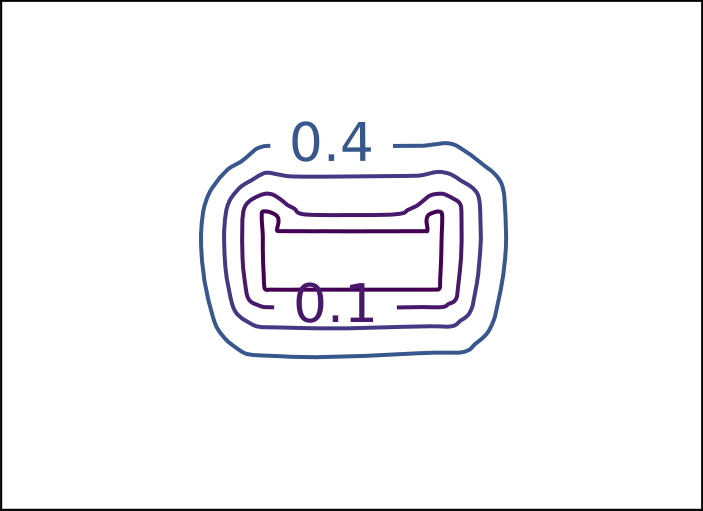
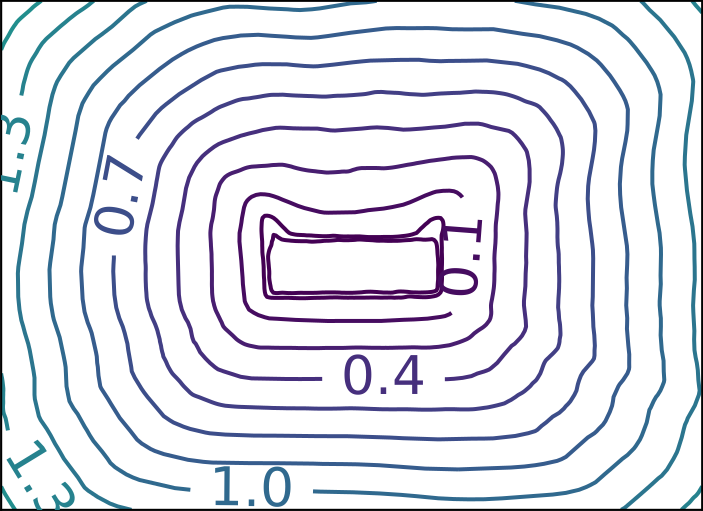


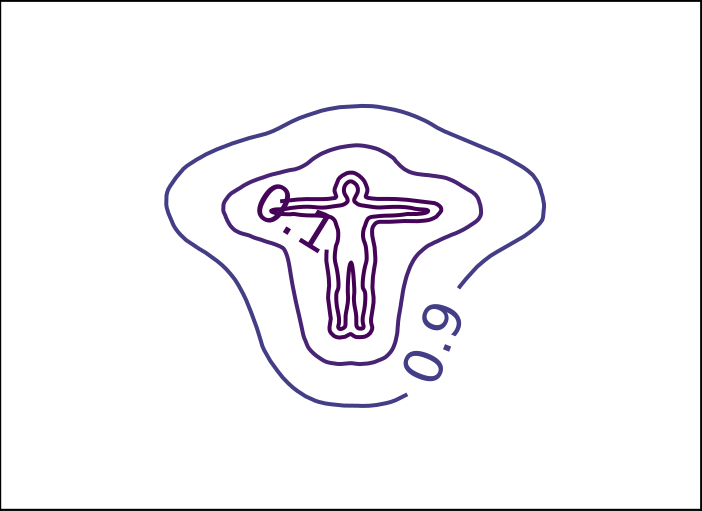
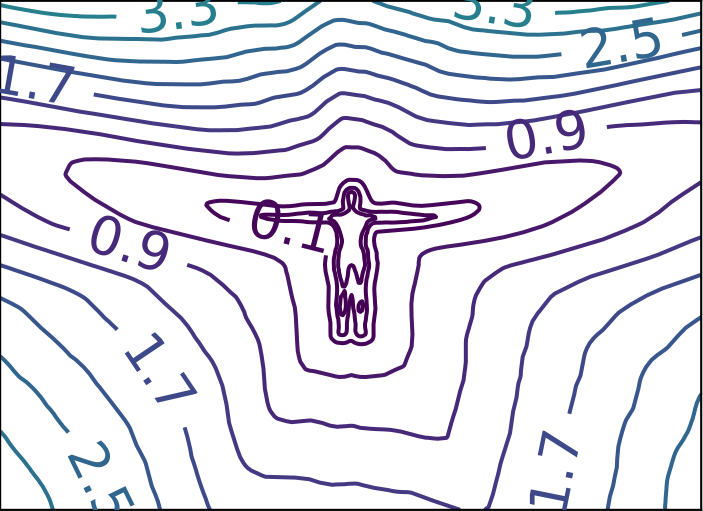
Ground Truth
ReDSDF
DeepSDF
ECMNN
Smooth Varying Distance Field in a Handover Scenario
Real World
Simulation
ATACOM + ReDSDF + SAC
Human Robot Interaction: Real-Sim
Human Robot Interaction
3x speed
Wrap Up
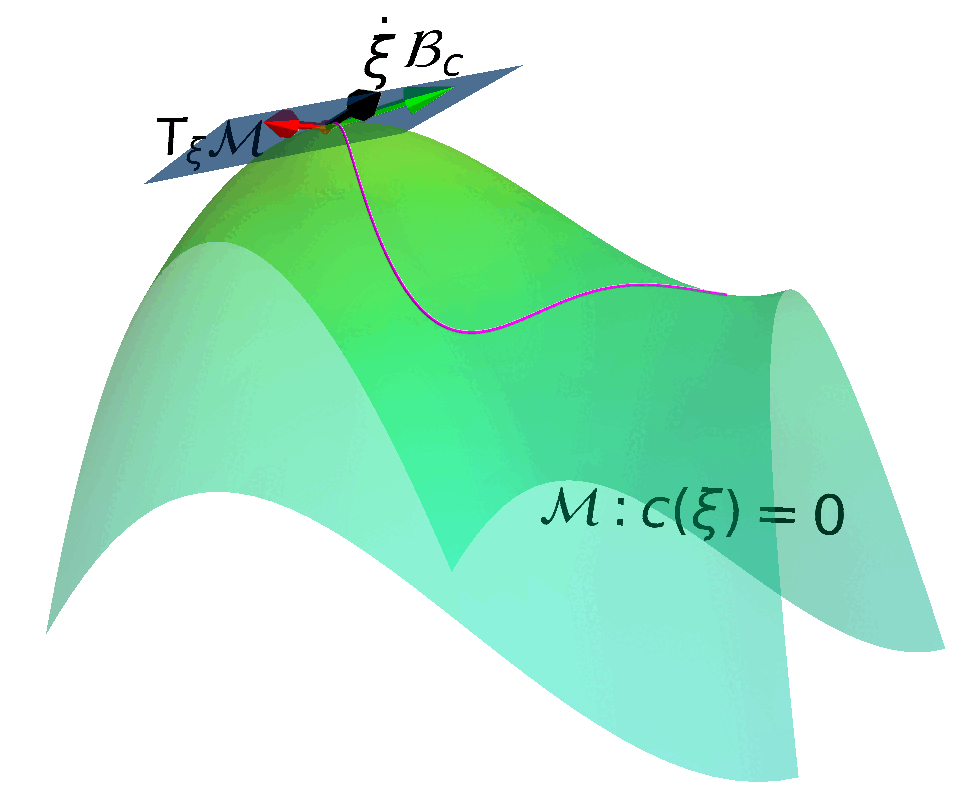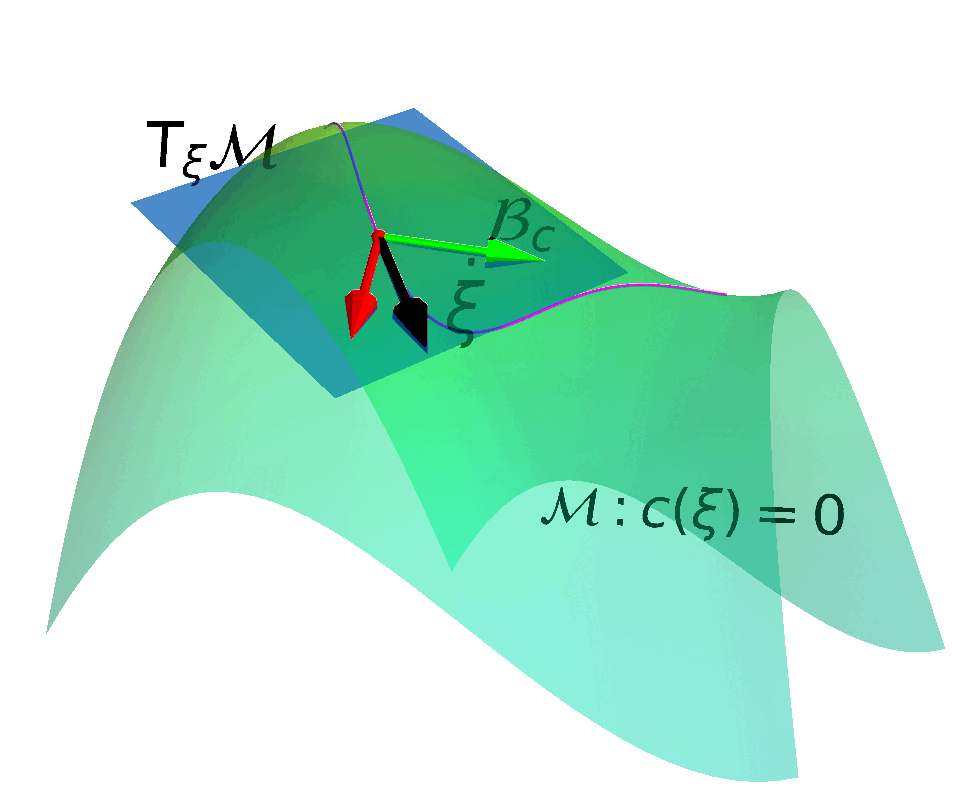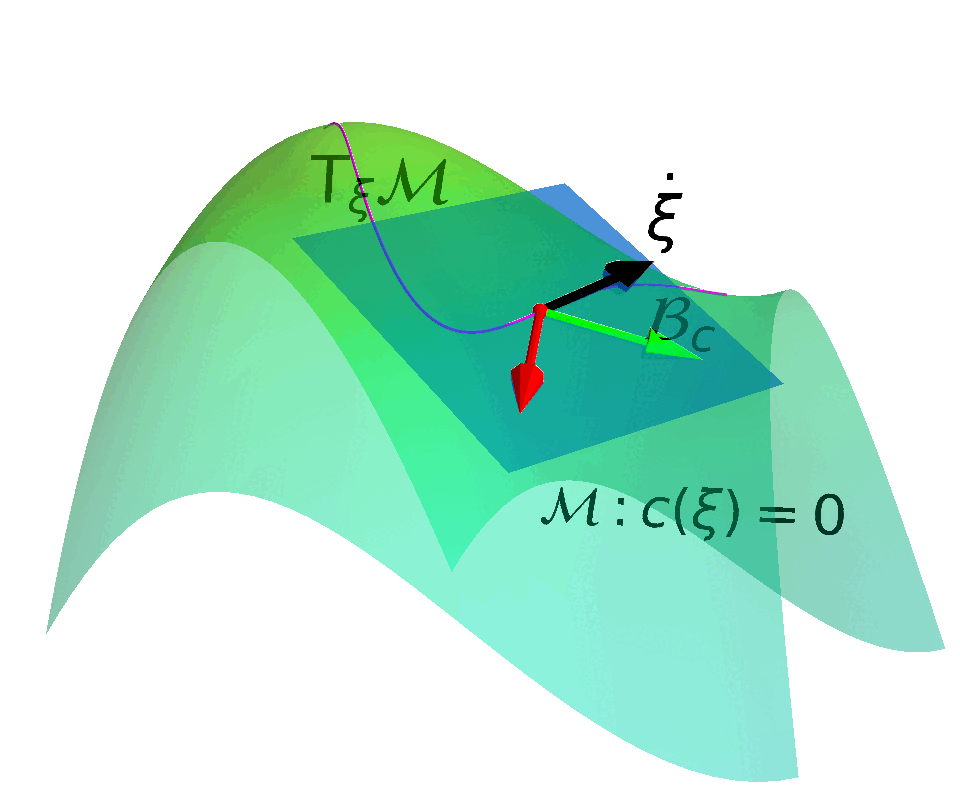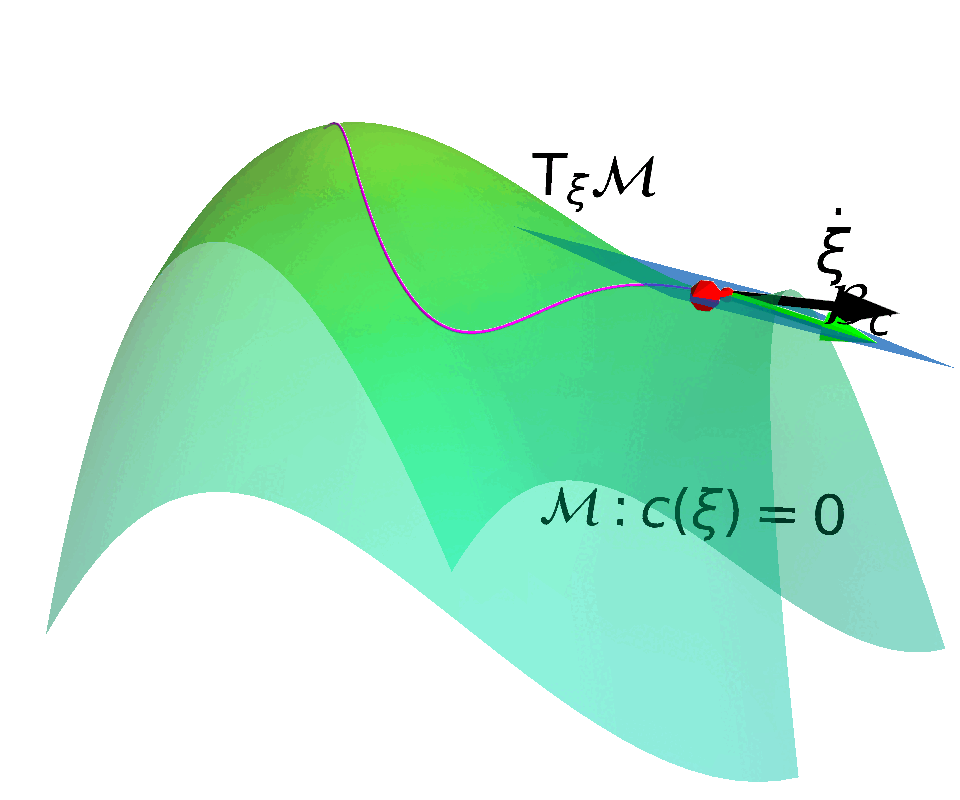
ATACOM: Safe Exploration on the Tangent Space of the Constraimt Manifold

Safe Exploration in Dynamic Environment

ReDSDF: Regularized Deep Signed Distance Field for Safe Learning and Control
