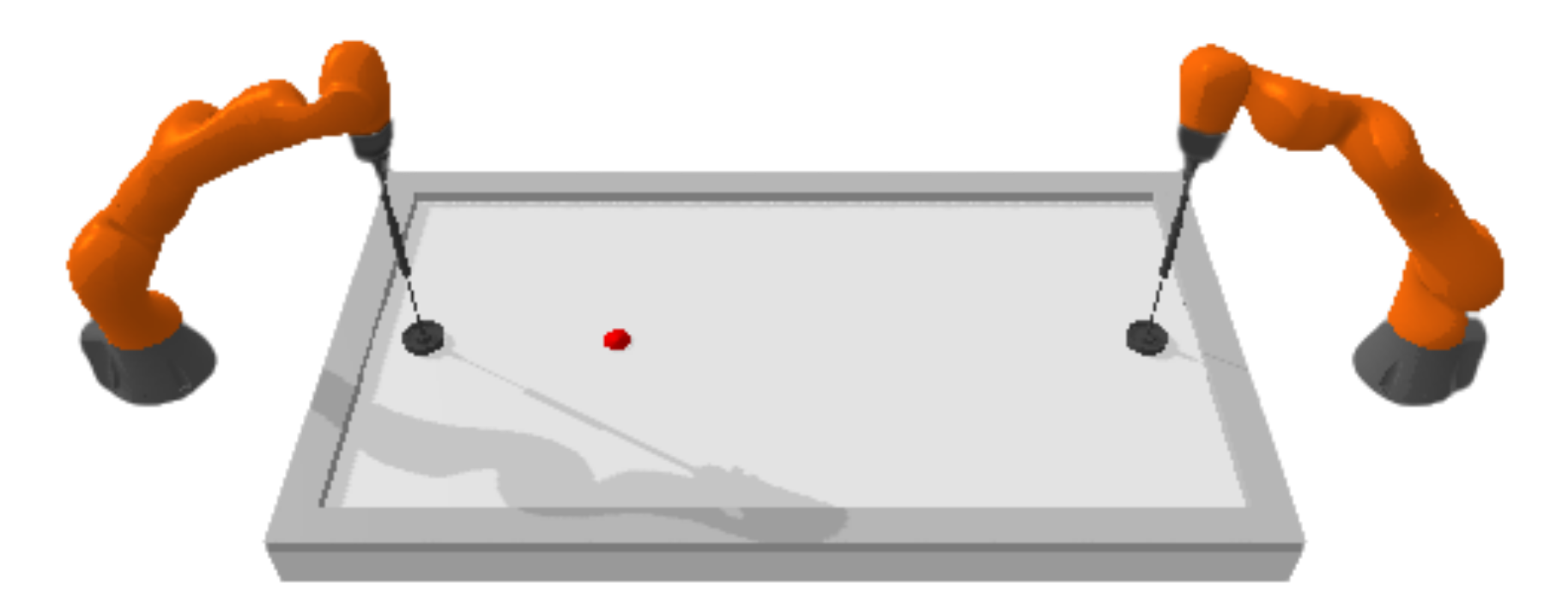
Robot Air Hockey
From System Engineering to Autonomous Intelligence
Puze Liu
Intelligent Autonomous Systems
Technical University Darmstadt
Analytical Robotics




Low Adaptability

Task Specific

Heavy Engineering
Endowing Robotics with Learning
Dexterous Manipulation, Open AI
Dexterous Manipulation, Open AI
Hutter M., Robotics Systems Lab, ETH
Dexterous Manipulation, Open AI
Hutter M., Robotics Systems Lab, ETH
Ploeger K., IAS, TU Darmstadt
Research Questions
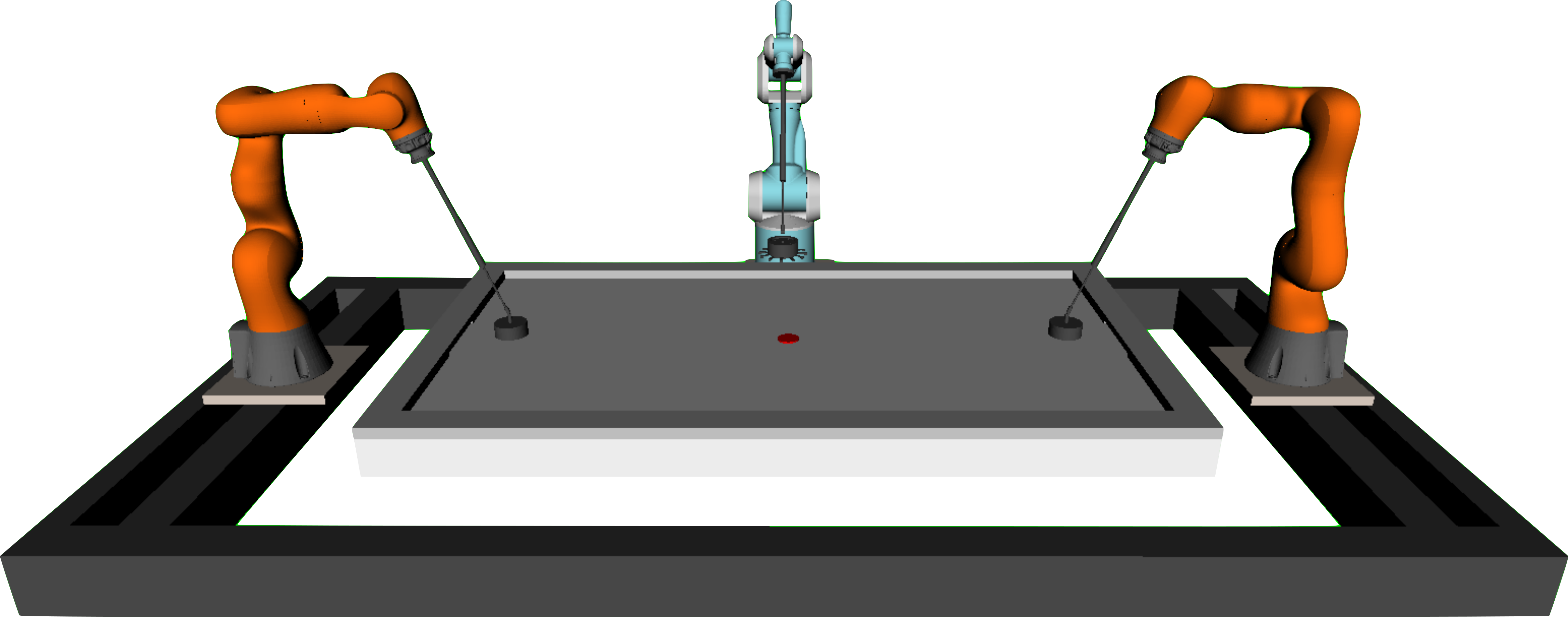
Learning vs Analytical Robotics:
What Can We Learn from the Air Hockey Challenge?
Baseline Agent
vs.
Learning Agent
Hardware



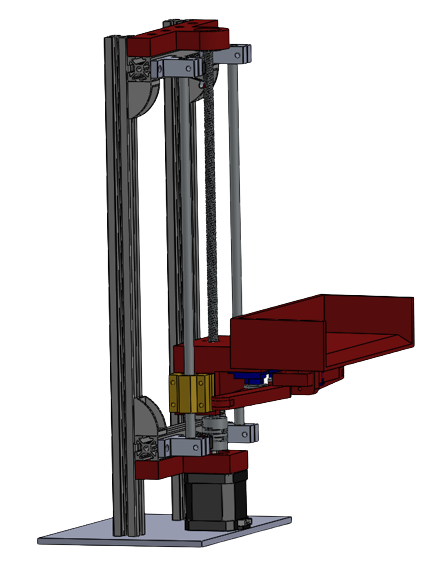






Baseline Agent

Baseline Agent
vs.
Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
Active Disturbance Rejection Control
- Accurate Tracking
- Compliant Controller
- Accessibility Limitations
- Dynamics Model
- Inbuilt Feedforward Dynamics
Baseline Agent

Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
How do we perform strong hitting?
Objective
Maximize the hitting velocity at the hitting point $\vp_h$ along the desired direction $\vv_h$
Constraints
For every trajectory point:
- EE stays on the table surface,
- EE stays inside the table boundary,
- Joint positions within the position limits,
- Joint velocities within the velocity limits.
Boundary conditions:
- Fixed starting position and velocity,
- Fixed hitting point and direction.
Additional Requirement:
- Solve in Real Time
Sequential Trajectory Optimizer
How do we perform strong hitting?
1. Hitting Configuration - NLP
$\begin{aligned} \max_{\vq} \quad &\| \vv_h^{\intercal} \mJ(\vq) \| + \lambda \| \vq - \vq_0\| \\ \text{s.t.} \quad & \text{FK}(\vq) = \vp_h \\ & \vq_{\text{min}} < \vq < \vq_{\text{max}} \end {aligned}$
Sequential Trajectory Optimizer
How do we perform strong hitting?
1. Hitting Configuration - NLP
$\begin{aligned} \max_{\vq} \quad &\| \vv_h^{\intercal} \mJ(\vq) \| + \lambda \| \vq - \vq_0\| \\ \text{s.t.} \quad & \text{FK}(\vq) = \vp_h \\ & \vq_{\text{min}} < \vq < \vq_{\text{max}} \end {aligned}$
$\vq^*$
2. Hitting Velocity - LP
$\begin{aligned} \max_{\dot{\vq}} \quad & \dot{\vq} \cdot \vv_h^{\intercal} \mJ(\vq^*) \\ \text{s.t.} \quad & \dot{\vq}_{\text{min}} < \dot{\vq} < \dot{\vq}_{\text{max}} \end {aligned}$
Sequential Trajectory Optimizer
How do we perform strong hitting?
1. Hitting Configuration - NLP
$\begin{aligned} \max_{\vq} \quad &\| \vv_h^{\intercal} \mJ(\vq) \| + \lambda \| \vq - \vq_0\| \\ \text{s.t.} \quad & \text{FK}(\vq) = \vp_h \\ & \vq_{\text{min}} < \vq < \vq_{\text{max}} \end {aligned}$
$\vq^*$
2. Hitting Velocity - LP
$\begin{aligned} \max_{\dot{\vq}} \quad & \dot{\vq} \cdot \vv_h^{\intercal} \mJ(\vq^*) \\ \text{s.t.} \quad & \dot{\vq}_{\text{min}} < \dot{\vq} < \dot{\vq}_{\text{max}} \end {aligned}$
$\vq^*$
3. Collision Free Planning
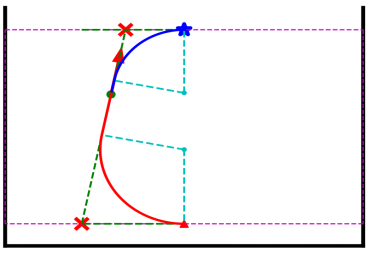
Sequential Trajectory Optimizer
How do we perform strong hitting?
1. Hitting Configuration - NLP
$\begin{aligned} \max_{\vq} \quad &\| \vv_h^{\intercal} \mJ(\vq) \| + \lambda \| \vq - \vq_0\| \\ \text{s.t.} \quad & \text{FK}(\vq) = \vp_h \\ & \vq_{\text{min}} < \vq < \vq_{\text{max}} \end {aligned}$
$\vq^*$
2. Hitting Velocity - LP
$\begin{aligned} \max_{\dot{\vq}} \quad & \dot{\vq} \cdot \vv_h^{\intercal} \mJ(\vq^*) \\ \text{s.t.} \quad & \dot{\vq}_{\text{min}} < \dot{\vq} < \dot{\vq}_{\text{max}} \end {aligned}$
$\vq^*$
4. Trajectory Optimization - QP
$ \begin{aligned} \max_{\valpha_i} \quad & \| \vb_i + \mN_{i}\valpha_i - \dot{\vq}^{a} \|_{W} \\ \text{s.t.} \quad & \dot{\vq}_{\text{min}} < \vb_i + \mN_{i}\valpha_i < \dot{\vq}_{\text{max}} \\ & \vq_{\text{min}} < \vq_{i-1} + (\vb_i + \mN_{i}\valpha_i)\mathrm{\Delta} t < \vq_{\text{max}} \\ \text{with} \quad & \mN_i = \text{Null}(\mJ(\vq_i)), \\ & \vb_i = \mJ^{\dagger}(\vq_i)\left[ \dot{\vx}_{i} + (\vx_{i} - \text{FK}(q_i)) / \mathrm{\Delta}t \right] \end{aligned} $
$\vx_{i}$
$\dot{\vx}_{i}$
3. Collision Free Planning

Sequential Trajectory Optimizer
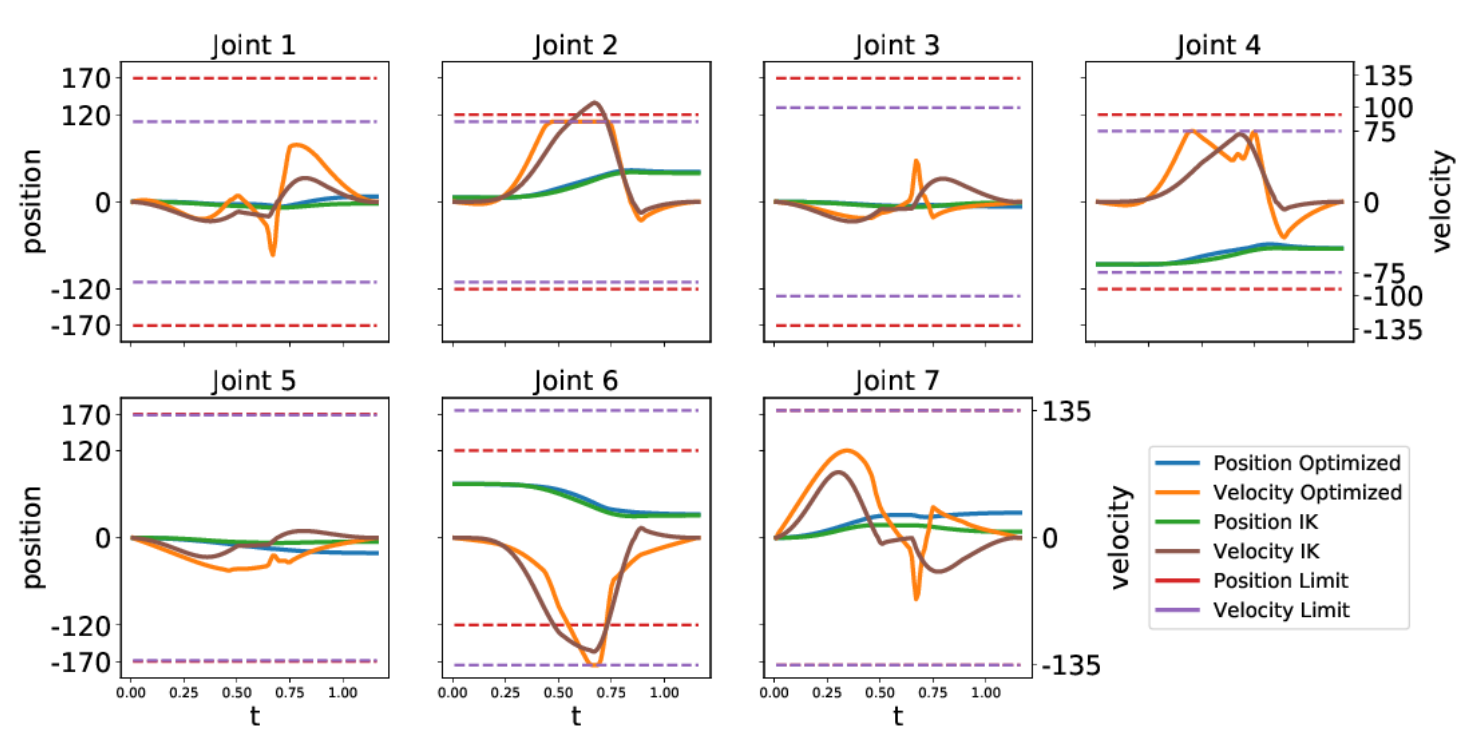
Optimization Result

Optimization Result
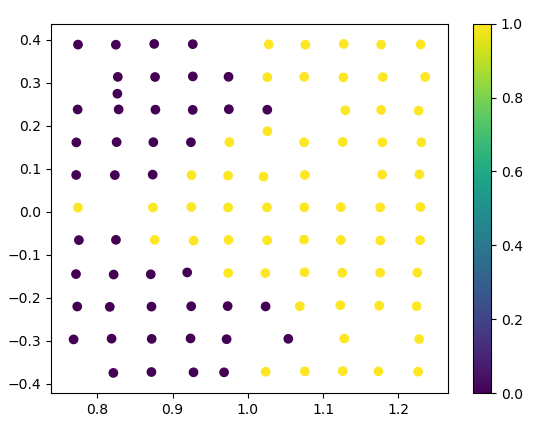
Success Rate: 53.6%
Baseline Agent

Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
Tactical Agent

Skill Library
Defend
Defend
Repel
Defend
Repel
Prepare
Baseline Agent

Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
High-Level Policy
Learning Collision Dynamics
System Identification
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
High-Level Policy
Learning Collision Dynamics
System Identification
Safe Reinforcement Learning
Problem Formulation
$$\begin{aligned} \max_{\pi} \quad & \bbE_{\tau \sim \pi}\left[ \sum_{t}^{T}\gamma^t r(\vs_t, \va_t) \right] \\ \text{s.t.} \quad & \mathcal{E}(\vs_t) = \vzero, \; \mathcal{I}(\vs_t) < \vzero, \; t\in[0, \cdots, T] \end{aligned}$$
$$\begin{aligned} \max_{\pi} \quad & \bbE_{\tau \sim \pi}\left[ \sum_{t}^{T}\gamma^t r(\vs_t, \va_t) \right] \\ \text{s.t.} \quad & \mathcal{E}(\vq_t, \vx_t) = \vzero, \; \mathcal{I}(\vq_t, \vx_t) < \vzero, \; t\in[0, \cdots, T] \\ & \vs_t = [\vq_t \;\; \vx_t] \end{aligned}$$
Problem Formulation
$$\begin{aligned} \max_{\pi} \quad & \bbE_{\tau \sim \pi}\left[ \sum_{t}^{T}\gamma^t r(\vs_t, \va_t) \right] \\ \text{s.t.} \quad & \mathcal{E}(\vq_t, \vx_t) = \vzero, \; \mathcal{I}(\vq_t, \vx_t) < \vzero, \; t\in[0, \cdots, T] \\ & \vs_t = [\vq_t \;\; \vx_t] \end{aligned}$$
Constraint Manifold
$$\MM_c = \left\{ (\vq, \vx, \vmu) \in \RR^{Q+E+I} \left| c(\vq, \vx, \vmu) = \begin{bmatrix} \mathcal{E}(\vq, \vx) \\ \mathcal{I}(\vq, \vx) + h(\vmu) \end{bmatrix} \right. = \vzero \right\}$$
$$h(\vmu)=\begin{bmatrix}h_0(\mu_0) \\ \cdots \\ h_I(\mu_I)\end{bmatrix}, \text{with} \; h_i:\RR \rightarrow \RR^+$$
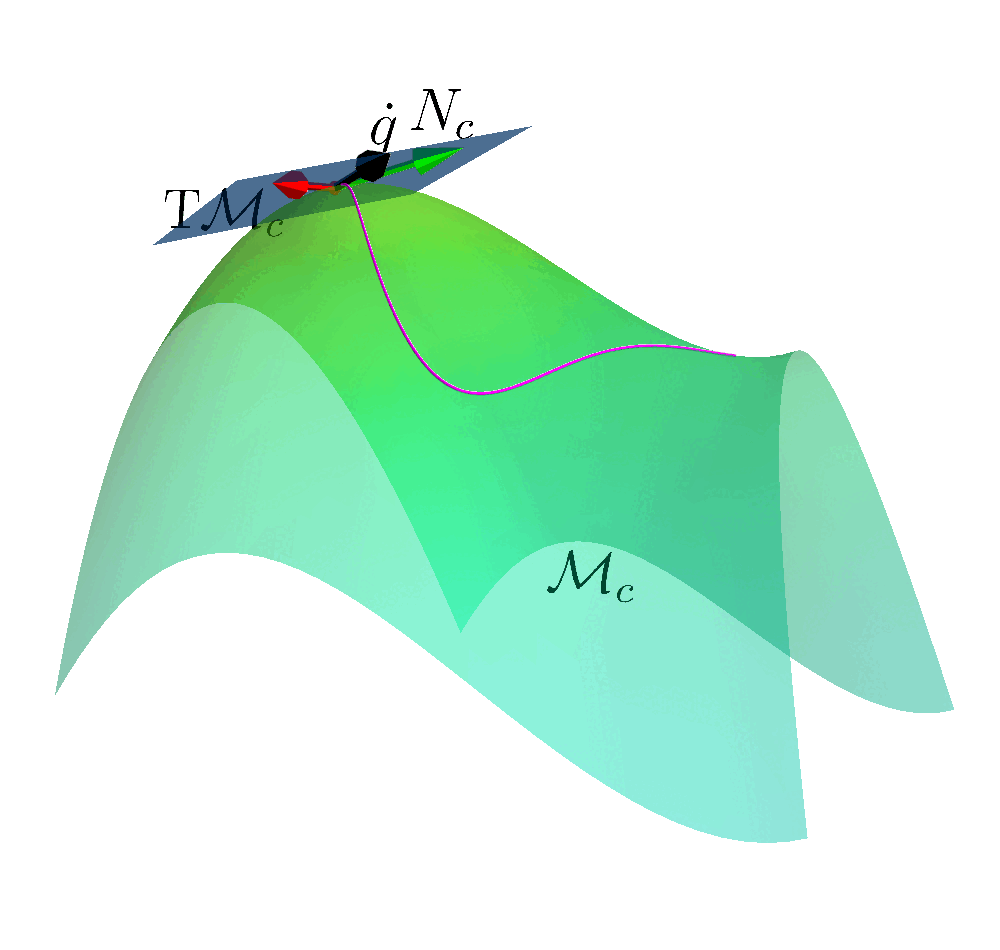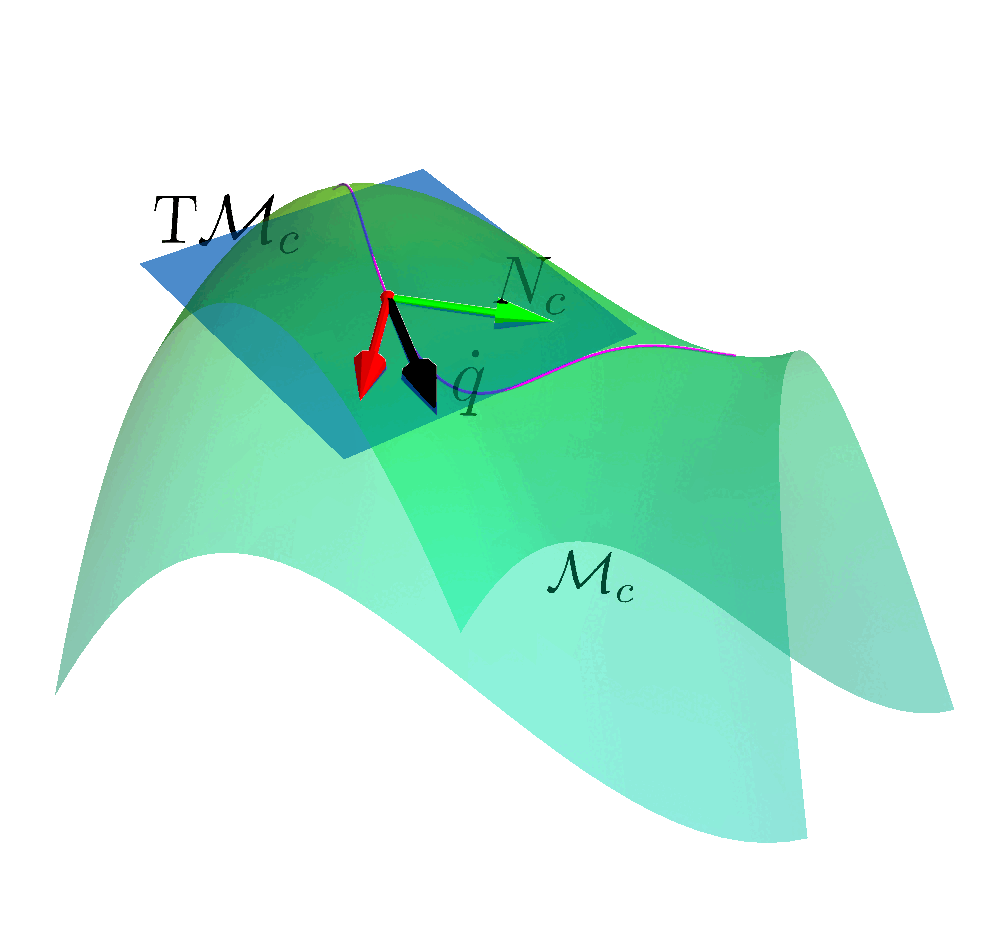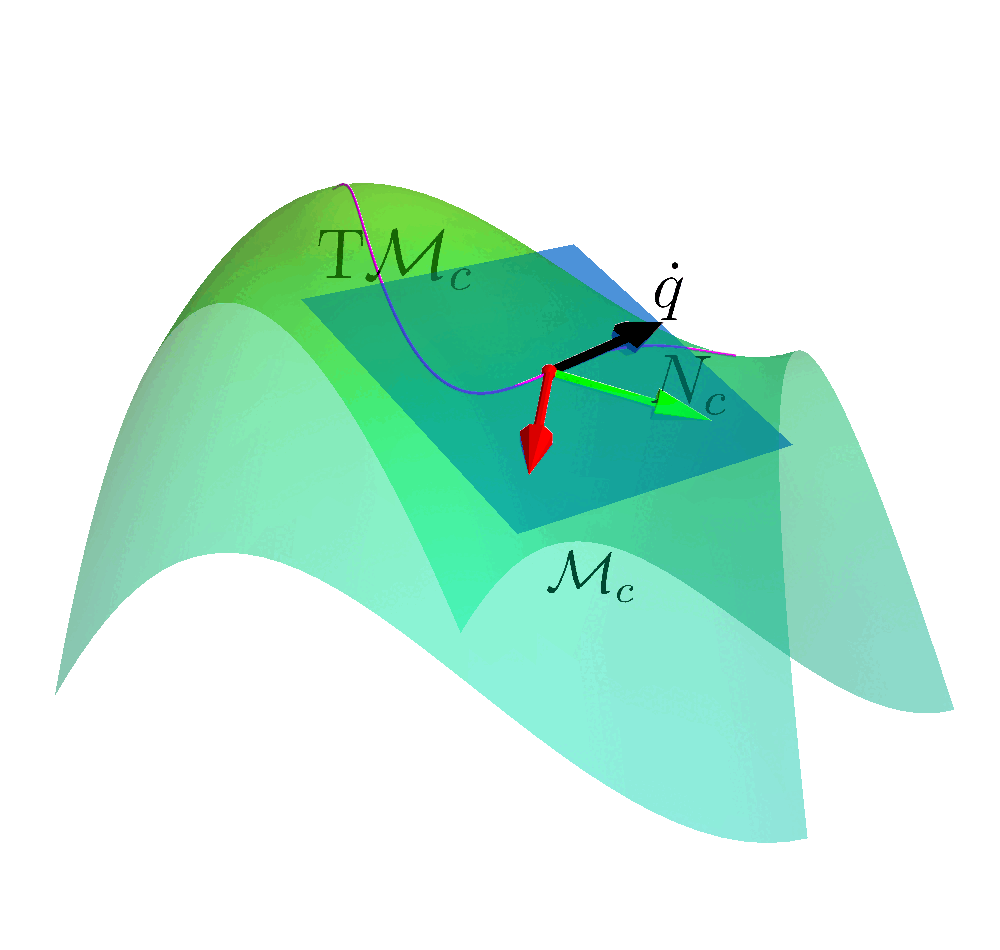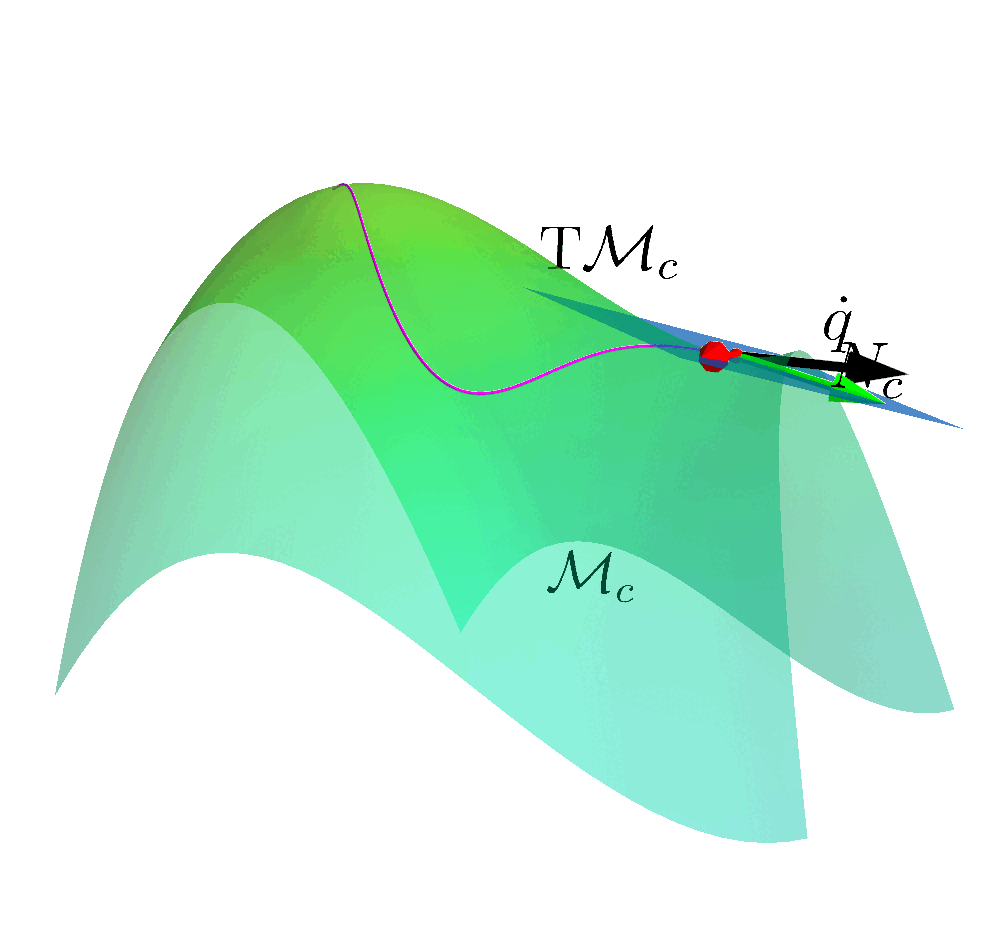
Safe Reinforcement Learning
Constraint Manifold
$$\MM_c = \left\{ (\vq, \vx, \vmu) \in \RR^{Q+E+I} \left| c(\vq, \vx, \vmu) = \begin{bmatrix} \mathcal{E}(\vq, \vx) \\ \mathcal{I}(\vq, \vx) + h(\vmu) \end{bmatrix} \right. = \vzero \right\}$$
Tangent Space
$$\mathrm{T}_{(q, x,\mu)}\MM_c = \left\{ (\dot{\vq}, \dot{\vx}, \dot{\vmu}) \left| \dot{c}(\vq,\vx,\vmu)= \mJ_q \dot{\vq} + \mJ_x \dot{\vx} + \mJ_{\mu}\dot{\vmu} = \vzero \right. \right\}$$
Nonlinear Control Affine System
$$\dot{\vq}=f(\vq) + G(\vq)\va$$
Tangent Space with Nonlinear Affine System
$$\mathrm{T}_{(q, x,\mu)}\MM_c = \left\{ (\va, \dot{\vx}, \dot{\vmu}) \left| \mJ_G\va + \mJ_{\mu}\dot{\vmu} + F(\vq, \vx, \dot{\vx}) = \vzero \right. \right\}$$
with $\mJ_G = \mJ_q G(q)$ and $F(\vq, \vx, \dot{\vx})=\mJ_q f(q) + \mJ_x \dot{\vx}$

Tangent Space with Nonlinear Affine System
$$\mathrm{T}_{(q, x,\mu)}\MM_c = \left\{ (\va, \dot{\vx}, \dot{\vmu}) \left| \mJ_G\va + \mJ_{\mu}\dot{\vmu} + F(\vq, \vx, \dot{\vx}) = \vzero \right. \right\}$$
We assume the $\dot{\vx}$ are known, estimated or zero.
Safe Controller
$\begin{bmatrix}\va \\ \dot{\vmu}\end{bmatrix} = \mN_{[G, \mu]} \textcolor{greenyellow}{\valpha} - \mJ^{\dagger}_{[G, \mu]}F(\vq, \vx, \dot{\vx})$
with $\mJ_{[G, \mu]} = [\mJ_G \; \mJ_{\mu}]$, $\mN_{[G, \mu]}=\text{Null}(\mJ_{[G, \mu]})$

Safe Reinforcement Learning


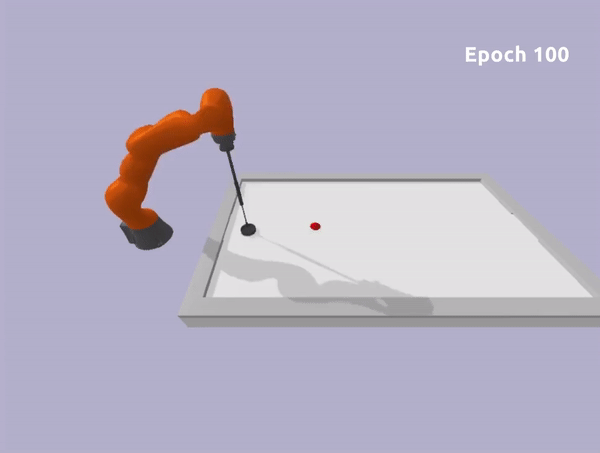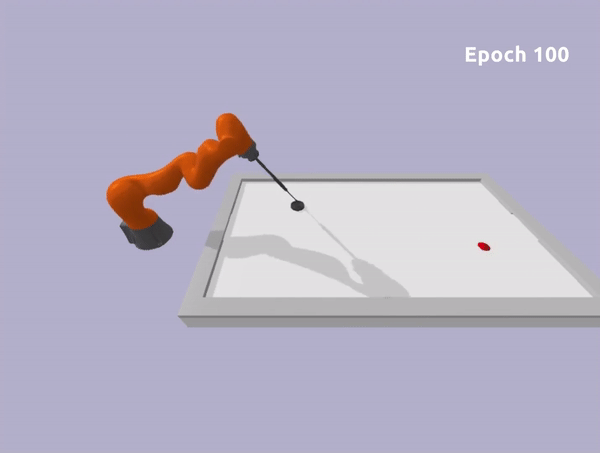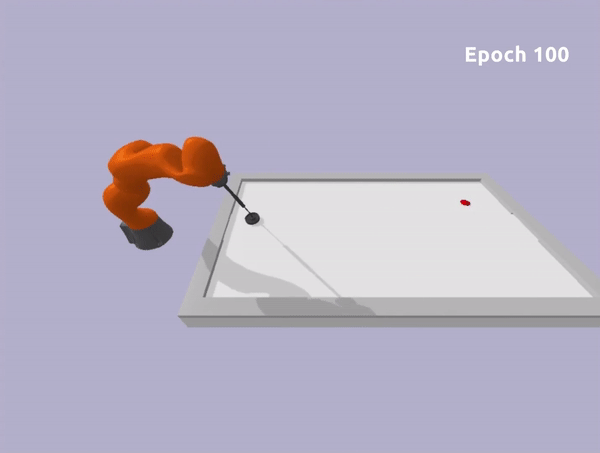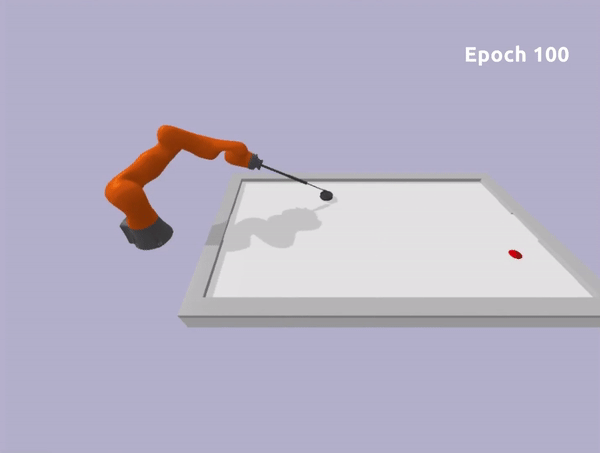
Safe Reinforcement Learning
Manipulation
Manipulation
Navigation
Manipulation
Navigation
Interaction

Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
High-Level Policy
Learning Collision Dynamics
System Identification
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
High-Level Policy
Learning Collision Dynamics
System Identification
Learn the Kinodynamic Planner
Requirement
- Plan Rapidly
- Satisfy the Contraints Stemming from the Robot's Kinematics and Environment
- Consider the Robot Dynamic Profile
- Perform Fast and Smooth Movements
Solution
- B-Spline in Joint Space
- Trajectory Knots Inferred from Neural Network
- Weighted Loss Considering Kinodynamic Properties and Constraints
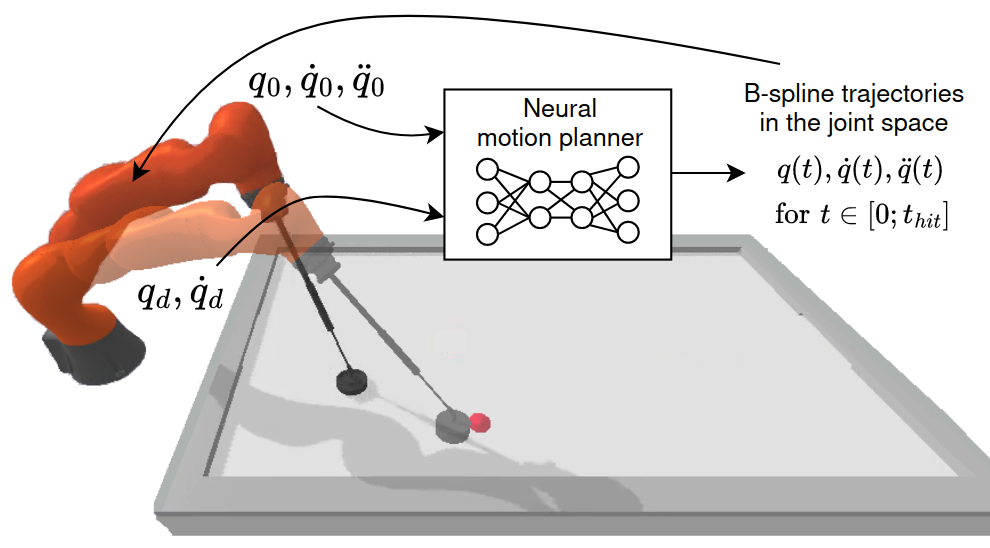
Learn the Kinodynamic Planner

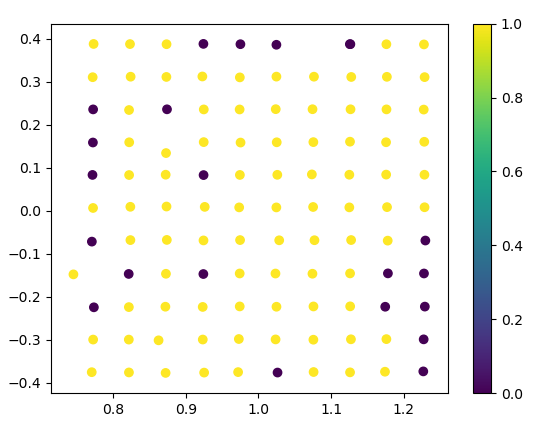


Lisjalous Hit


Lisjalous Hit
Dynamic Hit

Learning Agent
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
High-Level Policy
Learning Collision Dynamics
System Identification
Baseline Agent
Puck Tracking and Prediction
Trajectory Planner
vs.
Learning Agent
High-Level Policy
Learning Collision Dynamics
System Identification
Learning High-Level Tactics
Air Hockey Challenge - 2023